Support Vector Machines

As Support Vector Machines (SVM) são uma das técnicas mais utilizadas em Data Mining quando é necessário construir um classificador para dados constituídos maioritariamente por variáveis numéricas continuas/discretas.

A Ideia por detrás da SVM

A estratégia que a SVM implementa para construir um classificador é bastante simples: Se tivermos x bolas de duas cores podemos simplesmente colocar uma linha de forma a que se separem , isto permite-nos saber a partir desta informação que bolas acima da linha são azuis e bolas abaixo são vermelhas, o problema é que a linha pode estar em muitas posições diferentes e aparentemente esta não é a melhor e por isso recolocamos a linha de forma a que o classificador seja preciso . No entanto a realidade é que casos assim não existem, na verdade todos os casos que uma SVM classifica são sempre uma mistura de bolas azuis e vermelhas e por isso não existe nenhuma linha que separe estes casos mas de certeza que existe um plano! É por isso aumentamos uma (geralmente varias dimensões diferentes) dimensão para assim encontrar o plano que divide as bolas. Este passo é o mais complicado de entender pois sabemos que em duas dimensões o que é uma recta e em 3 dimensões um plano mas e em 4 ou em 6,7,20,50,1000 dimensões? É por isso que chamamos de hiperplano ao que separa as bolas vermelhas das azuis.

Como encontrar o hiperplano

Primeiro vamos assumir que cada bola é um objecto do tipo {<x1,x2,x3>,<y>} onde x* é os valores das variáveis e y a classe 1 ou -1, assim matematicamente o hiperplano é representado pela seguinte formula w.x*-b=0 onde w é vector de valores que queremos encontrar. Para isso precisamos de mais dois hiperplanos que serão os vectores de suporte estes hiperplanos são construídos a partir dos objectos que estão nas margens de cada classe,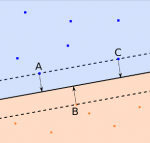 neste caso A,B e C. Apartir destes calculamos então o hiperplano que maximiza a distancia entre os dois hiperplanos de suporte. Sendo que w e b é igual para os 3 hiperplanos ficamos então com w.x*-b = 1 quando y=1 e w.x*-b = -1 quando y=-1 . Desta forma para sabermos qual a classe de um novo objecto so temos que ver qual o sinal do resultado da equação para x*.

Dimensões e Kernels

Dado que os dados nunca estão arranjados da forma que desejamos é necessário acrescentar dimensões, o problema disso é que dado que todas as contas feitas numa svm são produtos vectoriais , acrescentar uma dimensão tem consequências gravíssimas na performance do algoritmo. Para ultrapassar esse problema usa-se uma técnica chamada de Kernel Trick. Um kernel é uma forma de aumentar as dimensões sem ter que aumentar a complexidade, para isso é utilizada uma formula como a do Kernel Medico que faz a multiplicação vectorial de todos os objectos para uma matriz para assim a SVM utilizar estes resultados no calculo dos hiperplanos e ou durante a classificação.

Referências

https://www.reddit.com/r/MachineLearning/comments/15zrpp/please_explain_support_vector_machines_svm_like_i/ https://www.quantstart.com/articles/Support-Vector-Machines-A-Guide-for-Beginners