Compressão Lossless: diferenças entre revisões
(→PPM) |
|||
| (Há 135 revisões intermédias de 2 utilizadores que não estão a ser apresentadas) | |||
| Linha 1: | Linha 1: | ||
=História= | =História= | ||
A compressão de dados, que pode ser entendida como o processo de transformação de um conjunto de dados noutro conjunto de tamanho mais pequeno, começou a ganhar relevância durante a década de 80 e 90 e atualmente está presente em muitos aspetos do quotidiano. <ref>Nelson, M. (1991) The Data Compression Book. IDG Books Worldwide, Inc., Cambridge</ref> Curiosamente, com o desenvolvimento tecnológico exponencial destas décadas, o custo do armazenamento de dados diminuiu drasticamente, mas foi também durante este período que os algoritmos de compressão mais evoluíram. | A [[compressão de dados]], que pode ser entendida como o processo de transformação de um conjunto de dados noutro conjunto de tamanho mais pequeno, começou a ganhar relevância durante a década de 80 e 90 e atualmente está presente em muitos aspetos do quotidiano. <ref>Nelson, M. (1991) The Data Compression Book. IDG Books Worldwide, Inc., Cambridge</ref> Curiosamente, com o desenvolvimento tecnológico exponencial destas décadas, o custo do armazenamento de dados diminuiu drasticamente, mas foi também durante este período que os algoritmos de compressão mais evoluíram. | ||
A primeira vez que ficou registada uma utilização de um sistema de compressão foi a meio do século XIX por Samuel Morse no seu famoso código morse. Neste sistema de traços e pontos usados para comunicar à distância, Samuel Morse apercebeu-se que certas letras eram mais comuns do que outras, decidindo assim atribuir uma combinação de traços e pontos mais pequenas às letras mais comuns e combinações maiores às menos frequentes. A compressão de dados segue um processo muito semelhante. | A primeira vez que ficou registada uma utilização de um sistema de compressão foi a meio do século XIX por Samuel Morse no seu famoso [http://www.samuelmorse.net/ código morse]. Neste sistema de traços e pontos usados para comunicar à distância, Samuel Morse apercebeu-se que certas letras eram mais comuns do que outras, decidindo assim atribuir uma combinação de traços e pontos mais pequenas às letras mais comuns e combinações maiores às menos frequentes. A compressão de dados segue um processo muito semelhante. | ||
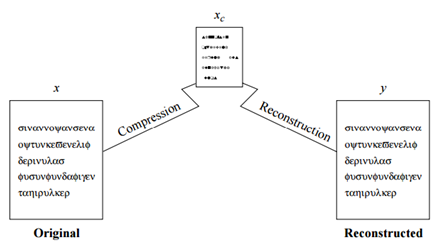
No entanto, só em 1948, Claude E. Shannon, através do seu trabalho “A Mathematical Theory of | No entanto, só em 1948, Claude E. Shannon, através do seu trabalho “A Mathematical Theory of Communication”<ref> Shannon, C., & Weaver, W. (1949) The Mathematical Theory of Communication. Urbana: University of Illinois Press</ref>, formalizou os conceitos de compressão de informação em termos teóricos.[http://math.harvard.edu/~ctm/home/text/others/shannon/entropy/entropy.pdf] Este artigo, entre vários conceitos matemáticos complexos, introduziu o conceito de compressão de informação dividida em duas vertentes, compressão lossless (onde não existe perda de informação) e [[compressão lossy]] (existe perda de informação durante o processo de compressão) como ilustrado na figura sendo que x=y para lossless e x≠y na lossy. Definiu também que uma compressão lossless iria estar limitada por um limite fundamental, definido pelo rácio de entropia. | ||
[[Ficheiro:A.png||Algoritmos lossless vs. lossy]] | |||
Lossless é então obtida através de um método de compressão onde é possível obter exatamente o mesmo conjunto de informação após descompressão, pois é um método não destrutivo. Contrastante com este método, a compressão Lossy é um método destrutivo, impossibilitando reverter | Lossless é então obtida através de um método de compressão onde é possível obter exatamente o mesmo conjunto de informação após descompressão, pois é um método não destrutivo. Contrastante com este método, a compressão Lossy é um método destrutivo, impossibilitando reverter | ||
Assim, ao longo dos anos, foram várias as empresas e cientistas que investiram muito no desenvolvimento de algoritmos de compressão para que hoje esteja presente em praticamente todos os aspetos da vida do ser humano, uma vez que muitos dos formatos mais comuns e genéricos do dia-a-dia são baseados em formas de compressão, desde as imagens, aos vídeos, passando pelos ficheiros “zipados”.<ref | Assim, ao longo dos anos, foram várias as empresas e cientistas que investiram muito no desenvolvimento de algoritmos de compressão para que hoje esteja presente em praticamente todos os aspetos da vida do ser humano, uma vez que muitos dos formatos mais comuns e genéricos do dia-a-dia são baseados em formas de compressão, desde as imagens, aos vídeos, passando pelos ficheiros “zipados”.<ref name="Salomon"/> | ||
“I have made these letters longer than usual because I lack the time to make it shorter” | <blockquote>''“I have made these letters longer than usual because I lack the time to make it shorter”'' | ||
::Blaise Pascal | |||
</blockquote> | |||
==Porquê compressão Lossless?== | ==Porquê compressão Lossless?== | ||
A necessidade de existirem métodos de compressão que consigam garantir a integridade dos dados é de elevada importância, pois por vezes, uma pequena diferença numa letra pode alterar substancialmente o significado de uma frase. Por exemplo as frases “Os rapazes, que comeram marisco, ficaram doentes” e “Os rapazes que comeram marisco ficaram doentes” ficam alteradas apenas pela adição de virgulas. Esta necessidade é exprimida por áreas onde a perda de dados pode originar problemas enormes, como imagem médica, dados de satélites, GPS, etc. <ref>Sayood, K. (2006) Introduction to Data Compression Third Edition. Morgan Kaufmann, Nebraska</ref> | A necessidade de existirem métodos de compressão que consigam garantir a integridade dos dados é de elevada importância, pois por vezes, uma pequena diferença numa letra pode alterar substancialmente o significado de uma frase. Por exemplo as frases “Os rapazes, que comeram marisco, ficaram doentes” e “Os rapazes que comeram marisco ficaram doentes” ficam alteradas apenas pela adição de virgulas. Esta necessidade é exprimida por áreas onde a perda de dados pode originar problemas enormes, como imagem médica, dados de satélites, GPS, etc. <ref>Sayood, K. (2006) Introduction to Data Compression Third Edition. Morgan Kaufmann, Nebraska</ref> | ||
<br> | |||
=Algoritmos Lossless= | =Algoritmos Lossless= | ||
| Linha 21: | Linha 25: | ||
Entre os algoritmos de compressão lossless mais famosos, são dignos de nota os LZ77 e LZ78 (também conhecidos como LZ1 e LZ2 respetivamente) não só pela importância cientifica, como pelo facto de serem a base de muitos outros algoritmos importantes. | Entre os algoritmos de compressão lossless mais famosos, são dignos de nota os LZ77 e LZ78 (também conhecidos como LZ1 e LZ2 respetivamente) não só pela importância cientifica, como pelo facto de serem a base de muitos outros algoritmos importantes. | ||
Estes dois algoritmos são codificadores de dicionário, o que significa que estes algoritmos operam através da procura de ligações entre os strings dos dados a comprimir e um set pré-determinado de strings numa estrutura de data - chamada dicionário. | Estes dois algoritmos são codificadores de dicionário, o que significa que estes algoritmos operam através da procura de ligações entre os strings dos dados a comprimir e um set pré-determinado de strings numa estrutura de data - chamada dicionário. | ||
A importância destes dois métodos ganha ainda mais relevância, pois foi devido a eles e aos seus pressupostos que mais tarde surgiram os modelos probabilísticos que começaram a criar mapas de probabilidades para serem codificados posteriormente, aumentando drasticamente a capacidade de compressão. | A importância destes dois métodos ganha ainda mais relevância, pois foi devido a eles e aos seus pressupostos que mais tarde surgiram os modelos probabilísticos que começaram a criar mapas de probabilidades para serem codificados posteriormente, aumentando drasticamente a capacidade de compressão.[http://ethw.org/History_of_Lossless_Data_Compression_Algorithms] | ||
==LZ77== | ==LZ77== | ||
O algoritmo da LZ77 atinge a compressão por trocar ocorrências repetidas com referência a uma única cópia existente numa certa posição anterior na corrente de dados. A principal característica deste algoritmo é que usa um método de janela deslizante. Esta janela vai acompanhando a leitura dos dados de input e está dividida em duas partes. A primeira parte é o bloco anterior ao caracter que está a ser lido – cursor - e irá funcionar como dicionário. A segunda parte é o bloco a seguir ao cursor, sendo que este também faz parte do bloco (lookahead buffer). Estes dois blocos são de comprimento fixo e embutidos no algoritmo. Ele é executado da seguinte forma:<ref>Blelloch, G. (2013) Introduction to Data Compression. Carnegie Mellon University</ref> <ref>Ziv, J., & Lempel, A. (1977). A universal algorithm for sequential data compression. IEEE Transactions on Information Theory</ref> | O algoritmo da LZ77 atinge a compressão por trocar ocorrências repetidas com referência a uma única cópia existente numa certa posição anterior na corrente de dados. A principal característica deste algoritmo é que usa um método de janela deslizante. Esta janela vai acompanhando a leitura dos dados de input e está dividida em duas partes. A primeira parte é o bloco anterior ao caracter que está a ser lido – cursor - e irá funcionar como dicionário. A segunda parte é o bloco a seguir ao cursor, sendo que este também faz parte do bloco (''lookahead buffer''). Estes dois blocos são de comprimento fixo e embutidos no algoritmo. Ele é executado da seguinte forma:<ref name="Introduction Data">Blelloch, G. (2013) Introduction to Data Compression. Carnegie Mellon University</ref> <ref>Ziv, J., & Lempel, A. (1977). A universal algorithm for sequential data compression. IEEE Transactions on Information Theory</ref> | ||
# Encontrar o maior match entre uma string que começa no cursor e está completamente embutida no lookahead buffer e uma string que começa no dicionário; | |||
# Devolve um valor triplo (p, n, c) onde p é a posição da ocorrência na janela, n é o comprimento do match e c o caracter após o match; | |||
# Mover o cursor n +1 caracteres para a frente. | |||
[[Ficheiro:B.png||Esquema do algoritmo LZ77]] | |||
No exemplo da imagem, onde o dicionário tem comprimento de 6 (negrito) e o lookahead de 4 (sublinhado) e a posição do cursor dentro do quadrado. A posição p pode ser 0, sendo que significa que não tem match, sendo 1 o primeiro caracter do dicionário (direita para esquerda). Caso encontre strings com tamanhos iguais, guarda o último por questões de performance. | No exemplo da imagem, onde o dicionário tem comprimento de 6 (negrito) e o lookahead de 4 (sublinhado) e a posição do cursor dentro do quadrado. A posição p pode ser 0, sendo que significa que não tem match, sendo 1 o primeiro caracter do dicionário (direita para esquerda). Caso encontre strings com tamanhos iguais, guarda o último por questões de performance. | ||
Para a descodificação, basta seguir as posições ao contrário e reconstruir. Um caso particular está na imagem no passo 3, em que n>p. O string a copiar está presente no ''lookahead buffer'' e, portanto, ao descodificar ainda não foi construído. O algoritmo corrige este problema repetindo o elemento até preencher n posições. | |||
==LZ78== | ==LZ78== | ||
O algoritmo LZ78 é mais conservador na adição de strings ao dicionário e atualmente a variante Lempel-Ziv-Welch (LZW) é a mais comum, dai ser a estudada neste trabalho. O primeiro passo deste algoritmo é formar o dicionário com um tamanho determinado pela memória disponível. Se forem 8 | O algoritmo LZ78 é mais conservador na adição de strings ao dicionário e atualmente a variante Lempel-Ziv-Welch (LZW) é a mais comum, dai ser a estudada neste trabalho. O primeiro passo deste algoritmo é formar o dicionário com um tamanho determinado pela memória disponível. Se forem 8 [[bit]]s, vai-se construir com as 255 primeiras entradas já ocupadas, sendo aumentado ao longo da leitura/codificação e pode ser traduzido com a seguinte interface:<ref name="Introduction Data"/> | ||
C’’ = AddDict (C, x) cria uma nova entrada no dicionário por aumentar uma entrada no dicionário existente pelo índex C com o byte x. Retorna novo índex | * C’’ = AddDict (C, x) cria uma nova entrada no dicionário por aumentar uma entrada no dicionário existente pelo índex C com o byte x. Retorna novo índex | ||
C’’ = GetIndex (C, x) retorna o índex de uma string por extensão de uma string correspondente ao índex C com o byte x. Se a entrada n existir, retorna -1 | * C’’ = GetIndex (C, x) retorna o índex de uma string por extensão de uma string correspondente ao índex C com o byte x. Se a entrada n existir, retorna -1 | ||
W = GetString (C) retorna a string W correspondente ao índex C | * W = GetString (C) retorna a string W correspondente ao índex C | ||
Flag = IndexInDict? (C) retorna verdadeiro se o índex C está no dicionário e falso caso contrário. | * Flag = IndexInDict? (C) retorna verdadeiro se o índex C está no dicionário e falso caso contrário. | ||
[[Ficheiro:C.png||Compressão LZ78]] | |||
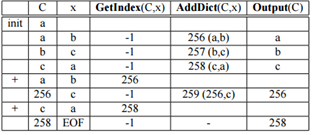
Para a compressão de “abcabca”, ele inicia a criação do dicionário e vai procurar por “a” que já existe. Como “a” já existe, vai procurar “ab” que não existe e por isso vai criar uma nova entrada no dicionário. Após esta criação vai procurar pelo segundo elemento que é o “b” que também vai existir no dicionário e por isso vai procurar “bc” que não vai existir no dicionário. Assim sendo irá criar uma nova entrada. O mesmo acontece para o “c” e “ca”. No entanto, quando procura de novo “a” após criar o “ca”, vai procurar “ab” que também existe e por isso, irá procurar “abc” que não irá existir e, por conseguinte, criar uma nova entrada., | Para a compressão de “abcabca”, ele inicia a criação do dicionário e vai procurar por “a” que já existe. Como “a” já existe, vai procurar “ab” que não existe e por isso vai criar uma nova entrada no dicionário. Após esta criação vai procurar pelo segundo elemento que é o “b” que também vai existir no dicionário e por isso vai procurar “bc” que não vai existir no dicionário. Assim sendo irá criar uma nova entrada. O mesmo acontece para o “c” e “ca”. No entanto, quando procura de novo “a” após criar o “ca”, vai procurar “ab” que também existe e por isso, irá procurar “abc” que não irá existir e, por conseguinte, criar uma nova entrada., | ||
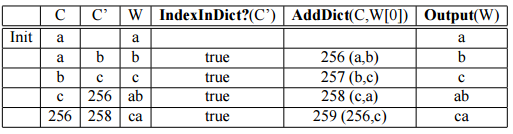
Para a descodificação, o algoritmo vai procurar as entradas no dicionário e devolve a string equivalente.<ref | Para a descodificação, o algoritmo vai procurar as entradas no dicionário e devolve a string equivalente.<ref name="Introduction Data" /> | ||
[[Ficheiro:D.png||Descompressão LZ78]] | |||
==Burrows-wheeler== | ==Burrows-wheeler== | ||
Este algoritmo, desenvolvido por Michael Burrows e David Wheeler em | Este algoritmo, desenvolvido por Michael Burrows e David Wheeler em 1943, é dos grandes algoritmos mais recentes e dos que consegue maiores ganhos de compressão, sendo também muito genérico, resulta muito bem em imagens, sons e texto. | ||
O funcionamento deste algoritmo é um pouco diferente dos referidos até agora que analisam o código a comprimir do início como um todo. Este método aborda os dados a comprimir dividido em blocos separados e codifica-os separadamente. A principal ideia por detrás deste algoritmo passa por transformar uma string S com n símbolos numa string L que satisfaça as seguintes condições:<ref> | O funcionamento deste algoritmo é um pouco diferente dos referidos até agora que analisam o código a comprimir do início como um todo. Este método aborda os dados a comprimir dividido em blocos separados e codifica-os separadamente. A principal ideia por detrás deste algoritmo passa por transformar uma string S com n símbolos numa string L que satisfaça as seguintes condições:<ref name="Introduction Data" /> | ||
# Cada região de L terá tendencialmente uma concentração de poucos símbolos. Ou seja, se encontrarmos um certo símbolo em L, deveremos encontrar outras instâncias do mesmo por perto. Assim este string poderá ser eficientemente comprimido com outros métodos como ''move-to-front'', RLE ou os já vistos anteriormente. De notar que este método só se torna eficaz a partir de valores elevados de n. | |||
# A possibilidade de reconstruir S a partir de L. | |||
[[Ficheiro:E.png||Algoritmo Burrows-wheeler]] | |||
As possibilidades de permutações de símbolos são fatoriais, por isso as possibilidades são enormes, mesmo em casos de poucos símbolos, o que torna vital a escolha adequada das permutações a realizar. | As possibilidades de permutações de símbolos são fatoriais, por isso as possibilidades são enormes, mesmo em casos de poucos símbolos, o que torna vital a escolha adequada das permutações a realizar. | ||
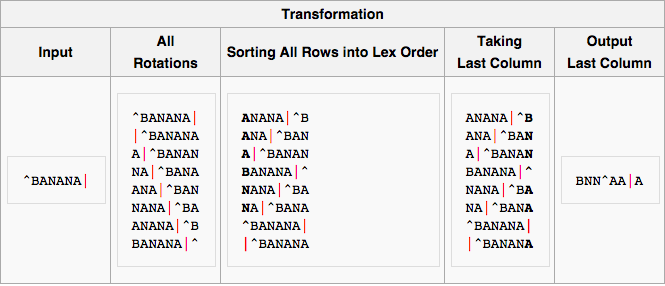
Assim sendo, este método irá começar por criar uma matriz de “n x n” em que n é o tamanho do bloco a ser comprimido, sendo que a primeira linha é o texto original e a seguinte sofre uma translação/shift para a esquerda uma posição, incrementando a translação por 1 a cada linha até termos a translação até n-1. Após isto, ordena-se a matriz por ordem alfabética. Desta matriz retiramos a última coluna (que irá sempre preencher o requisito 1) e guardamos a valor da linha original para poder descodificar. A última coluna e a localização da linha original é então enviado para o codificador. | Assim sendo, este método irá começar por criar uma matriz de “n x n” em que n é o tamanho do bloco a ser comprimido, sendo que a primeira linha é o texto original e a seguinte sofre uma translação/''shift'' para a esquerda uma posição, incrementando a translação por 1 a cada linha até termos a translação até n-1. Após isto, ordena-se a matriz por ordem alfabética. Desta matriz retiramos a última coluna (que irá sempre preencher o requisito 1) e guardamos a valor da linha original para poder descodificar. A última coluna e a localização da linha original é então enviado para o codificador. | ||
Para a descodificação, após reconstruir a coluna escolhida para a compressão suplementar, conseguimos facilmente criar a primeira coluna (devido à ordenação léxica). A primeira e última coluna juntas dão-nos a informação necessária para reconstruir pois temos todos os pares de caracteres e a sua sequência. Esta informação permite construir um vetor para as seguintes colunas e a informação guardada da linha original permite reconstruir tudo. | Para a descodificação, após reconstruir a coluna escolhida para a compressão suplementar, conseguimos facilmente criar a primeira coluna (devido à ordenação léxica). A primeira e última coluna juntas dão-nos a informação necessária para reconstruir pois temos todos os pares de caracteres e a sua sequência. Esta informação permite construir um vetor para as seguintes colunas e a informação guardada da linha original permite reconstruir tudo. | ||
==PPM== | ==PPM== | ||
Não sendo um algoritmo de compressão propriamente dito, mas antes um algoritmo de previsão, o PPM (prediction by partial matching) é usado, entre outras coisas, para fins de compressão de dados. O conceito é elegantemente simples, tendo, no entanto, implementações bem complexas. O algoritmo consegue retornar a probabilidade de distribuição do próximo símbolo a ser codificado, tendo em conta os dados anteriores, semelhante ao formato do dicionário da LZ77, aqui chamada de contexto.<ref>Cleary, J., & Witten, I. (1984). Data Compression Using Adaptive Coding and Partial String Matching. IEEE Transactions on Communications</ref> | Não sendo um algoritmo de compressão propriamente dito, mas antes um algoritmo de previsão, o [[PPM]] (''prediction by partial matching'') é usado, entre outras coisas, para fins de compressão de dados. O conceito é elegantemente simples, tendo, no entanto, implementações bem complexas. O algoritmo consegue retornar a probabilidade de distribuição do próximo símbolo a ser codificado, tendo em conta os dados anteriores, semelhante ao formato do dicionário da LZ77, aqui chamada de contexto.<ref name="IEEE">Cleary, J., & Witten, I. (1984). Data Compression Using Adaptive Coding and Partial String Matching. IEEE Transactions on Communications</ref> | ||
Comparando com a língua portuguesa, sabemos que a letra “u” é pouco comum, mas é extremamente comum que apareça depois de um “q”. O mesmo acontece ao contrário: uma consoante a seguir a um “q” é extremamente improvável (para não dizer impossível) na língua portuguesa. Estes casos são muito simples com diferenças de probabilidades enormes, mas a capacidade deste algoritmo passa por detetar tendências mais suaves nos conjuntos de 1 e 0. No entanto, o uso de contextos grandes iria requerer um grande número de cálculos e capacidade de armazenamento das probabilidades condicionais calculadas, o que poderia comprometer o uso do algoritmo. Para fazer face a esta dificuldade, o PPM executa este procedimento faseadamente ao longo da leitura.<ref | Comparando com a língua portuguesa, sabemos que a letra “u” é pouco comum, mas é extremamente comum que apareça depois de um “q”. O mesmo acontece ao contrário: uma consoante a seguir a um “q” é extremamente improvável (para não dizer impossível) na língua portuguesa. Estes casos são muito simples com diferenças de probabilidades enormes, mas a capacidade deste algoritmo passa por detetar tendências mais suaves nos conjuntos de 1 e 0. No entanto, o uso de contextos grandes iria requerer um grande número de cálculos e capacidade de armazenamento das probabilidades condicionais calculadas, o que poderia comprometer o uso do algoritmo. Para fazer face a esta dificuldade, o PPM executa este procedimento faseadamente ao longo da leitura.<ref name="IEEE" /> <ref name="Salomon">Salomon, D. & Motta, G. (2010) Handbook of Data Compression Fifth Edition. Springer-Verlag London, California </ref> | ||
Como um exemplo de compressão de texto, suponhamos que o algoritmo está a analisar um contexto de ordem 3 “dos” que apareceu 27 vezes no passado e 11 vezes foi seguido por um espaço, 9 vezes por uma “s”, 6 vezes por um “e” e 1 vez por um “i”. Se o símbolo a codificar for um espaço, é enviado para o codificador aritmético com uma probabilidade de 11/27 e as probabilidades são atualizadas para 12/28, 9/28, 6/28 e 1/28. Se o símbolo fosse diferente destes (por exemplo um “p”) passaríamos para a ordem 2 (“os”), 1 (“s”), 0 que são as vezes que simplesmente apareceu um ”p” no passado e se mesmo assim nunca tivesse aparecido um “p”, passaríamos para contexto -1 e seria codificado com 1/(tamanho do alfabeto). Ordem -1 é muito comum no início da codificação.<ref | O PPM é chamado um [[modelo de contexto adaptativo]] porque usa o contexto exatamente precedente ao caracter a codificar e não uma tabela fixa. Ele começa por analisar o contexto C precedente ao caracter S de ordem n (ou tamanho de n caracteres). Caso não encontre no conjunto de dados já processado um contexto C seguido de caracter S, ele assume probabilidade de 0 e recomeça com um contexto de tamanho n-1. Quando a probabilidade é maior que 0, envia para o codificador o símbolo S com probabilidade P.<ref name="Salomon" /> | ||
Para se conseguir descodificar, a alteração da ordem do contexto tem de ficar contabilizada e perfeitamente indicada, pois descodificador não sabe qual é o caracter seguinte. Isto é feito através de um escape | Como um exemplo de compressão de texto, suponhamos que o algoritmo está a analisar um contexto de ordem 3 “dos” que apareceu 27 vezes no passado e 11 vezes foi seguido por um espaço, 9 vezes por uma “s”, 6 vezes por um “e” e 1 vez por um “i”. Se o símbolo a codificar for um espaço, é enviado para o codificador aritmético com uma probabilidade de 11/27 e as probabilidades são atualizadas para 12/28, 9/28, 6/28 e 1/28. Se o símbolo fosse diferente destes (por exemplo um “p”) passaríamos para a ordem 2 (“os”), 1 (“s”), 0 que são as vezes que simplesmente apareceu um ”p” no passado e se mesmo assim nunca tivesse aparecido um “p”, passaríamos para contexto -1 e seria codificado com 1/(tamanho do alfabeto). Ordem -1 é muito comum no início da codificação.<ref name="Salomon" /> | ||
Para se conseguir descodificar, a alteração da ordem do contexto tem de ficar contabilizada e perfeitamente indicada, pois descodificador não sabe qual é o caracter seguinte. Isto é feito através de um ''escape symbol'' para o descodificador saber que tem de reduzir a ordem do contexto. Assim no caso referido em cima, quando o codificador chega a um contexto de ordem -1, vindo de um de ordem 3, deve antes ter codificado 4 ''escape symbols'' antes. | |||
[[Ficheiro:F.png||Algoritmo PPM]] | |||
(1 | Seguindo o exemplo da figura, assumindo que “assanissimassa” já foi codificado e está-se a utilizar uma ordem de contexto 2 (“sa” portanto), podem acontecer 1 de 4 alternativas baseadas no caracter a seguir:<ref name="Salomon" /> | ||
# Caso fosse “n”, o algoritmo já tinha encontrado “sa” seguido por um “n” e, portanto, iria enviar a probabilidade (1/2) | |||
# Caso fosse “s”, o algoritmo nunca viu “sa” seguido de um “s”, e iria, portanto, descer um nível de ordem de contexto que passaria a “a” e enviaria para o codificador um ''escape symbol'' com probabilidade (1/2). Como o codificador já viu um “a” seguido de um “s”, envia com a probabilidade associada (2/5) | |||
# Caso fosse “m”, o algoritmo não iria encontrar match nos contextos de ordem 2 nem 1 por isso passaria para o contexto 0 (enviando dois ''escape symbols'') e mandaria o “m” sozinho e a sua probabilidade (1/19) | |||
Salomon | # Finalmente temos o caso de ser por exemplo um “d” que o algoritmo nunca viu. Por isso nenhuma das ordens de contexto anteriores iria encontrar ''match'' e, portanto, iriam ser codificados 3 ''escape symbols'' e enviaria o “m” com a probabilidade de 1/28 (todo o alfabeto/hipóteses)<ref name="Salomon" /> | ||
==PAQ e Content-mixing== | ==PAQ e Content-mixing== | ||
O PAQ é um algoritmo open-source veio trazer alguma disrupção ao mundo da compressão. Este algoritmo de alta-performance baseado em context-mixing está atualmente no topo dos rankings de compressão, apesar de ter um custo elevado de memória e tempo (quem tem vindo a ser combatida). Mas a grande revolução está associada ao facto de ser open-source e permitir muitas versões, subversões, derivações e spin-offs. O uso de context-mixing tem sido o principal objeto de intervenção e desenvolvimento nos últimos tempos, principalmente devido à aplicação de conceitos experimentais de machine-learning. | O [[PAQ]] é um algoritmo ''[[open-source]]'' veio trazer alguma disrupção ao mundo da compressão. Este algoritmo de alta-performance baseado em ''context-mixing'' está atualmente no topo dos ''rankings'' de compressão, apesar de ter um custo elevado de memória e tempo (quem tem vindo a ser combatida). Mas a grande revolução está associada ao facto de ser ''[[open-source]]'' e permitir muitas versões, subversões, derivações e ''spin-offs''. O uso de ''[[context-mixing]]'' tem sido o principal objeto de intervenção e desenvolvimento nos últimos tempos, principalmente devido à aplicação de conceitos experimentais de [[machine-learning]]. | ||
De certa forma este formato teve origem através do PPM e do Burrows-Wheeler , uma vez que é baseado em distribuição algorítmica. No entanto existem duas grandes diferenças:<ref>Blaszczy, K. (2012) PAQ compression algorithm. RWTH Aachen University</ref> <ref>Mahoney, M. (2005) Adaptive Weighing of Context Models for Lossless Data Compression. Florida Tech. Technical Report CS-2005-16, Florida</ref> | De certa forma este formato teve origem através do PPM e do Burrows-Wheeler , uma vez que é baseado em distribuição algorítmica. No entanto existem duas grandes diferenças:<ref name="PAQ">Blaszczy, K. (2012) PAQ compression algorithm. RWTH Aachen University</ref> <ref>Mahoney, M. (2005) Adaptive Weighing of Context Models for Lossless Data Compression. Florida Tech. Technical Report CS-2005-16, Florida</ref> | ||
# O contexto passa a ser uma função complexa dos dados já vistos; | |||
# Ao invés de um único modelo previsor, existem vários modelos. | |||
O PAQ consegue ultrapassar algumas das limitações do PPM, não requisitando que os contextos sejam contíguos. Context-mixing entra neste modelo na medida em que o PAQ não usa apenas um modelo de probabilidades, mas vários que posteriormente cruza e atribui pesos diferentes. Os principais modelos de contexto são:<ref | O PAQ consegue ultrapassar algumas das limitações do PPM, não requisitando que os contextos sejam contíguos. ''Context-mixing'' entra neste modelo na medida em que o PAQ não usa apenas um modelo de probabilidades, mas vários que posteriormente cruza e atribui pesos diferentes. Os principais modelos de contexto são:<ref name="PAQ" /> <ref name="Salomon" /> | ||
* ''n-grams''; em que é baseado nos últimos n bytes antes do símbolo a prever (tal como o PPM); | |||
* ''whole-word n-grams'', ignorando letras maiúsculas e caracteres não alfabéticos (útil em texto); | |||
* Contextos ''“sparse”'' que apenas conta o segundo e quarto byte antes do símbolo a prever (útil em alguns formatos binários); | |||
* Contextos analógicos, consistindo em [[bit]]s de ordem elevada 8-16 bit (útil em multimédia); | |||
* Modelos especializados que são executados quando um certo formato de ficheiro é detetado. | |||
A união dos resultados destes modelos irá originar a probabilidade a codificar para o caracter. A probabilidade é ponderada tendo em conta os pesos dos modelos. A título de exemplo, do PAQ1 ao PAQ3, as várias probabilidades eram combinadas por somatório ponderado, sendo que era atribuído um peso superior aos contextos mais longos. | A união dos resultados destes modelos irá originar a probabilidade a codificar para o caracter. A probabilidade é ponderada tendo em conta os pesos dos modelos. A título de exemplo, do PAQ1 ao PAQ3, as várias probabilidades eram combinadas por somatório ponderado, sendo que era atribuído um peso superior aos contextos mais longos. | ||
Do PAQ4 ao 6, eram atribuídos | Do PAQ4 ao 6, eram atribuídos maiores pesos aos contextos mais exatos e finalmente a partir do PAQ7, as probabilidades eram atribuídas usando redes neurais. <ref name="PAQ" /> <ref name="Salomon" /> | ||
=Formatos de ficheiros= | =Formatos de ficheiros= | ||
Entre os formatos de compressão mais conhecidos, o que é sem duvida mais conhecido é o “.zip”. Este formato está amplamente difundido a nível mundial pela sua capacidade de compressão, rapidez e compatibilidade. Este formato foi criado por Phil Katz em 1989 e consegue utilizar vários algoritmos, mas usa essencialmente DEFLATE que é baseado no LZ77 e que também foi desenvolvido por Katz. Consegue comprimir até 16 exabytes de ficheiros. 9 | Entre os formatos de compressão mais conhecidos, o que é sem duvida mais conhecido é o “.zip”. Este formato está amplamente difundido a nível mundial pela sua capacidade de compressão, rapidez e compatibilidade. Este formato foi criado por Phil Katz em 1989 e consegue utilizar vários algoritmos, mas usa essencialmente [[DEFLATE]] que é baseado no LZ77 e que também foi desenvolvido por Katz. Consegue comprimir até 16 exabytes de ficheiros. 9 | ||
O formato .rar também tem tido alguma popularidade pelo publico geral e é baseado nos algoritmos de Lempel-Ziv e PPM. Foi criado por Eugene Roshal, sendo que é dai que deriva o seu nome – | O formato .rar também tem tido alguma popularidade pelo publico geral e é baseado nos algoritmos de Lempel-Ziv e [[PPM]]. Foi criado por Eugene Roshal, sendo que é dai que deriva o seu nome – '''R'''oshal '''AR'''chive. Os programas usados são o RAR e o WinRAR que oferecem completo suporte para .rar e .zip. Consegue também descomprimir um conjunto de outros formatos, mas não comprimir. Consegue comprimir até 8,6 biliões de gigabytes (ou qualquer coisa como 7.8 zettabytes).<ref name="Salomon" /> | ||
=Benchmark= | =Benchmark= | ||
Para se perceber de que maneira se fazem as comparações entre algoritmos, é preciso perceber alguns conceitos que serão comuns a todos. | Para se perceber de que maneira se fazem as comparações entre algoritmos, é preciso perceber alguns conceitos que serão comuns a todos. | ||
São eles rácio de compressão, fator de compressão e ganhos de compressão. | São eles rácio de compressão, fator de compressão e ganhos de compressão.<br> | ||
O rácio é uma fórmula simples e intuitiva:<ref>Salomon, D., | O rácio é uma fórmula simples e intuitiva:<ref name="Salomon" /> | ||
''Rácio de compressão=(Tamanho do output) / (Tamanho do input)'' | |||
Esta também é reconhecida por [[bit]] per bit, porque irá traduzir na quantidade de [[bit]]s necessários para traduzir um [[bit]] do input. A expressão 100x (1- rácio de compressão) é usada como intermutável com o rácio, embora neste caso um valor de 80% indicará que o resultado ocupa 20% do original. | |||
O fator de compressão é o rácio elevado a -1 ou:<ref name="Salomon" /> | |||
''Fator de compressão=(Tamanho do input)/(Tamanho do output)'' | |||
Neste momento no topo em termos de capacidade de compressão estão os algoritmos baseados em [[context-mixing]] como nanozip, modificações da [[PAQ]] e do [[PPM]] que já conseguem valores de compressão ao nível do bit por byte, como se pode verificar em sites especializados nestes testes como o [http://imagecompression.info/ imagecompression] e o [http://www.squeezechart.com/ squeezechart]. | |||
Atualmente existe um concurso chamado de [http://prize.hutter1.net/ ''“Hutter Prize”''], iniciado em 2006 por Marcus Hutter, onde a candidatura é aberta a toda a gente e oferece 500 euros por cada 1% de compressão adicional sobre o atual vencedor. O ficheiro a comprimir é o enwik8 que se baseia nos primeiros 100 000 000 caracteres da wikipedia em inglês<ref name="Hutter"/>. Os últimos 3 algoritmos vencedores foram da autoria de Alexander Rhatushnyak com versões do [[PAQ]].<ref name="Hutter">http://prize.hutter1.net/ (acedido dia 05/04/2017)</ref> | |||
=Compressão de dados em Saúde= | |||
A imagem médica tem sido um dos campos de maior desenvolvimento no que diz respeito a aplicações biomédicas. Por conseguinte, a compressão sem perdas surge como fundamental nesta área, pois toda a informação contida num ''[[pixel]]'' é de extrema importância. Contudo, é essencial que esse processo possua uma elevada taxa de compressão bem como a capacidade de descodificar os dados comprimidos em várias resoluções. Esses dados são armazenados em sistemas de arquivo computorizados como [[PACS]] (''Picture Archiving and Communication System'') e [[DICOM]] (''Digital Imaging and Communications in Medicine''), seguindo sempre as normas internacionais [[HL7]] para a troca de informação em forma de texto.<ref name="Badshah">Badshah, G., Liew, S., Zain, J. M., Hisham, S. I., & Zehra, A. (2015). Importance of Watermark Lossless Compression in Digital Medical Image Watermarking. Research Journal of Recent Sciences, 4(3), 75–79.</ref><ref name="Janet">Janet, J., Mohandass, D., & Meenalosini, S. (2011). Lossless Compression Techniques for Medical Images in Telemedicine. Advances in Telemedicine:Technologies, Enabling Factors and Scenarios, 111–131. | |||
</ref><ref name="Anusuya">Anusuya, V., Raghavan, V. S., & Kavitha, G. (2014). Lossless Compression on MRI Images Using SWT. Journal of Digital Imaging, 27(5), 594–600. https://doi.org/10.1007/s10278-014-9697-9</ref> | |||
Estes desenvolvimentos levaram a um aumento exponencial da quantidade de dados médicos, pois a obtenção de imagens cada vez mais frequente e o seu tamanho é cada vez maior (como visto na imagem em baixo). Este aumento tornou imprescindível o desenvolvimento de técnicas para armazenamento, gestão e proteção das mesmas, pois cada vez mais as imagens médicas são armazenadas digitalmente, principalmente na área da radiologia.<ref name="Scholl">Scholl et al., Challenges of medical image processing. | |||
Comput Sci Res Dev (2011) 26: 5–13</ref> <ref name="Janet" /> | |||
[[Ficheiro:L-compressao.PNG|| Volumes de dados para diagnóstico médico<ref name="Scholl" />]] | |||
Torna-se assim necessário arranjar métodos eficazes para a gestão desta quantidade de informação sem ocupar espaços digitais gigantescos.<ref name="GONZALEZ">Gonzalez, R. C. & Woods, R. E. “Digital Image Processing”. Addison-Wesley Publishing Company, 1992.</ref> | |||
Uma redução na quantidade de espaço necessário para o armazenamento de dados traz muitas vantagens como a redução da largura de banda, do custo e do tempo necessários para a transmissão de dados, potencializando análises mais rápidas e fáceis à distância. <ref name="Janet" /> | |||
==Mecanismos de compressão ''lossless'' de imagens Raio-x== | |||
Desde 1895 (ano da sua descoberta) até à atualidade, as imagens obtidas por radiação x continuam a ser uma ferramenta importante no diagnóstico médico. Contudo, a [[telemedicina]] trouxe a necessidade de armazenar e transmitir eficientemente essas imagens. O método que de seguida se descreve elimina os dados que não pertencem à região de interesse na imagem de raio-x. Os pixéis de fundo não contém informações médicas relevantes e, portanto, serão removidos. A região de interesse será separada dos pixéis de fundo e posteriormente comprimida por compressão lossless, promovendo assim uma redução do tamanho da imagem bipartido, pela remoção de informação e pela compressão em si . A segmentação seguida de compressão torna-se difícil de atingir pelo facto de existirem regiões cuja intensidade não é uniforme entre o osso e partes moles nas imagens de radiologia convencional. Métodos de segmentação baseados em bordas, como ''Canny'' e ''Sobel'', quando aplicados a imagens de raio-x não apresentaram uma eficaz segmentação. Embora não haja um método 100% fiável na extração da região de interesse nas imagens de raio-x, ''Kazeminia'' e seus colaboradores desenvolveram um método para extração da região de interesse que se baseia na análise de distribuição dos pixéis de fundo nas imagens. Primeiramente é encontrada a intensidade que separa a região de interesse da região de não interesse, para depois ser atribuído o mesmo valor à intensidade dos pixéis dessa região de não interesse. <ref name="Kazeminia">Kazeminia, S., Karimi, N., Soroushmehr, S. M. R., Samavi, S., Derksen, H., & Najarian, K. (2015). Region of interest extraction for lossless compression of bone X-ray images. Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, 2015–November, 3061–3064. https://doi.org/10.1109/EMBC.2015.7319038</ref> <ref name="GONZALEZ" /> | |||
[[Ficheiro:G-extrac.png|| Imagem original de raio-x b) Extração da região de interesse com o Watershed c) Segmentação da imagem com crescimento de região d) Extração da região de interesse com o método thresholding e) Deteção de bordas com o método Canny f) Suavização da imagem com filtro Gaussiano <ref name="Kazeminia" />]] | |||
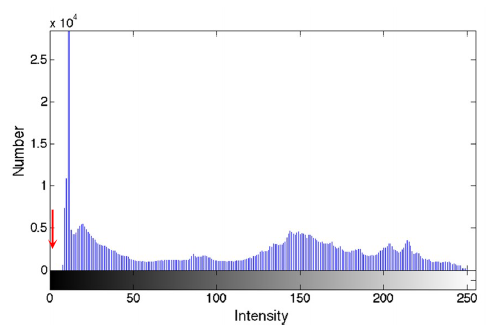
O ruído inevitavelmente existente nas imagens de raio-x e que influencia as regiões de interesse pode ser removido com recurso a [[filtros Gaussianos]]. A deteção da região de interesse é feita com recurso ao histograma da imagem. Os valores abaixo da concavidade negativa do histograma são separados dos restantes que correspondem à região de interesse (representado pela seta vermelha no gráfico da figura). É aplicada uma máscara binária, transformando em 0 todos os pixéis abaixo desse limiar da concavidade negativa do histograma (isto porque esses pixéis não têm dados importantes). Os píxeis acima desse limiar assumem o valor 1. <ref name="Kazeminia" /> <ref name="GONZALEZ" /> | |||
[[Ficheiro:E-compressao.png]] | |||
Para comprimir os dados da máscara binária referida constituída por 0 e 1, é usada a técnica de codificação ''[[run-lenght]]'' (RLE), útil quando há sequências longas de carateres iguais. Numa primeira fase, RLE converte a imagem numa sequência e depois faz o cálculo do número de valores semelhantes até encontrar um valor diferente. Dadas as sequências longas de 0 e 1, a técnica [[RLE]] torna-se eficiente nesta máscara binária. <ref name="Kazeminia" /> 18 | |||
Pixéis vizinhos nas regiões de interesse têm intensidades semelhantes, logo pode concluir-se que há redundância espacial. Assim sendo, essa redundância espacial pode ser convertida em redundância estatística pelo preditor [[ALCM]] (''activity level classification model''), que tem sido implementado na compressão de imagens 3D obtidas por ressonância magnética. <ref name="Kazeminia" /> | |||
O valor do ''[[pixel]]'' atual no [[ALCM]] é predito por uma combinação linear de alguns dos píxeis vizinhos que já estão processados. Os pesos desta combinação linear são calculados à medida que a codificação prossegue. O mesmo peso é inicialmente atribuído a todos os píxeis envolvidos. Após a predição ser realizada, os pesos poderiam mudar da seguinte maneira: Se o valor previsto fosse menor que o valor real do ''[[pixel]]'' então 1/256 é subtraído do peso do maior ''[[pixel]]'' da vizinhança e adicionado ao peso do menor. Se o valor predito fosse maior do que o ''[[pixel]]'' real, então o peso do ''[[pixel]]'' da vizinhança maior é aumentado em 1/256 e o peso do menor é reduzido. <ref name="Kazeminia" /> | |||
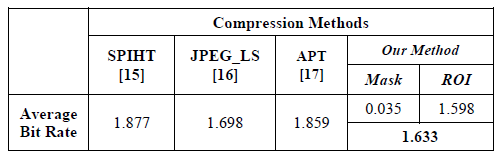
Após aplicação do algoritmo em MatLab 2013 e testado em 60 imagens de raio-x, o método de compressão descrito tem a taxa mais baixa de ''[[bits]]'' mesmo quando comparada com métodos como [[SPIHT]], [[JPEG-LS]] e [[APT]]. <ref name="Kazeminia" /> <ref name="Rema">Rema, N. R., Oommen, B. A., & Mythili, P. (2015). Image compression using SPIHT with modified spatial orientation trees. Procedia Computer Science, 46(Icict 2014), 1732–1738. https://doi.org/10.1016/j.procs.2015.02.121</ref> | |||
[[Ficheiro:H-compressao.png||Comparação entre métodos de compressão de dados sem perda]] | |||
==Compressão em mamografia== | |||
À semelhança do que foi referido para as imagens ósseas obtidas por raio-x, também na mamografia existem grandes benefícios com o armazenamento digital eficaz das imagens e da fácil transmissão das mesmas. Para se ter uma ideia do espaço necessário, o estudo ''standard'' da incidência oblíqua médio-lateral e crânio-caudal podem ocupar 120 ''Megabytes'' em disco. No final de um dia, o espaço requerido para as mamografias realizadas é demasiado, sendo de extrema utilidade a compressão sem perda de dados.<ref name="Marques">Marques, J. R. T., Honório, T. C. S., Kees, J., Souza, A. R. C. De, & Batista, L. V. (2007). Compressão sem Perdas de Imagens Mamográficas Utilizando Código ''Gray'' e Algoritmo PPM, 1216–1217.</ref> | |||
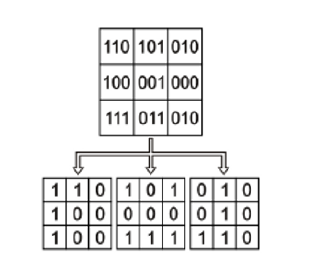
Este método irá decompor a imagem mamográfica em planos de ''[[bits]]'' para de seguida os comprimir separadamente pelo PPM adaptado ao alfabeto binário para os requisitos computacionais serem ainda menores. A decomposição em plano de ''[[bit]]s'' decompõe uma imagem S de n ''[[bit]]s por [[pixel]]'' (ou seja, 2n níveis de cinza) em n imagens binárias, ou planos de ''[[bit]]s'', s0, s1, …, sn-1. Um ''[[pixel]]'' no plano si equivale ao i-ésimo bit do ''[[pixel]]'' nas mesmas coordenadas em S. A figura seguinte ilustra, a título de exemplo, essa decomposição em três planos.<ref name="Marques" /> <ref name="Zhang">Zhang, Y., & Adjeroh, D. A. (2008). Prediction by partial approximate matching for lossless image compression. IEEE Transactions on Image Processing, 17(6), 924–935. https://doi.org/10.1109/TIP.2008.920772</ref> | |||
[[Ficheiro:I-compressao.png]] | |||
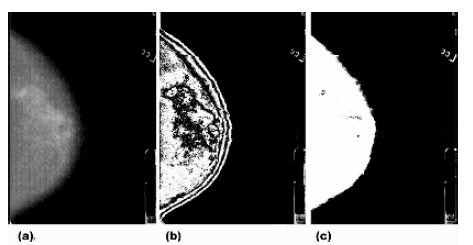
Para separar a região da mama do ''background'' foi efetuada a segmentação por limiarização. Seja X um valor escolhido com as características do ''background'' da mama. Os píxeis com valor maior que X são classificados como mama, os restantes correspondem ao ''background''.<ref name="Marques" /> | |||
[[Ficheiro:J-compressao.png||a)Imagem original b) plano de ''bits'' s8 c) plano de ''[[bits]]'' s10]] | |||
Para permitir a descompressão correta dos dados, uma imagem binária será adicionada ao arquivo comprimido: de valor 1 indicará a região da mama e de valor 0 indicará o ''background''.<ref name="Marques" /> | |||
A representação binária usada foi o código ''Gray'' onde dois números sucessivos se distinguem por um ''bit''. Por norma, nas imagens médicas dois valores consecutivos não variam significativamente devido à natureza contínua dos sinais originais e, por tal razão, a compressão por planos de ''[[bit]]s'' é mais eficaz. Essa variação é reduzida com o código ''Gray'': pela análise da tabela observa-se que na transição 3-4 no código convencional binário todos os ''[[bit]]s'' alteraram enquanto no código ''Gray'' só o primeiro sofreu alteração.<ref name="Marques" /> | |||
[[Ficheiro:K-compressao.png||Redução da informação com o código Gray numa imagem de mamografia. a) sem código ''Gray'' b) com código ''Gray'' c) Plano de ''[[bit]]s'': sem código ''Gray'' d) Plano de ''[[bit]]s'': com código ''Gray'']] | |||
= Este conteúdo em vídeo = | |||
<p align="justify">Caso pretenda a visualização deste conteúdo em vídeo clique [https://uporto.cloud.panopto.eu/Panopto/Pages/Viewer.aspx?id=3f0a0a18-b904-4dcf-ab18-b3897e7d61ea aqui].</p> | |||
=Referências Bibliográficas= | |||
<references/> | <references/> | ||
Edição atual desde as 21h16min de 7 de junho de 2017
História
A compressão de dados, que pode ser entendida como o processo de transformação de um conjunto de dados noutro conjunto de tamanho mais pequeno, começou a ganhar relevância durante a década de 80 e 90 e atualmente está presente em muitos aspetos do quotidiano. [1] Curiosamente, com o desenvolvimento tecnológico exponencial destas décadas, o custo do armazenamento de dados diminuiu drasticamente, mas foi também durante este período que os algoritmos de compressão mais evoluíram. A primeira vez que ficou registada uma utilização de um sistema de compressão foi a meio do século XIX por Samuel Morse no seu famoso código morse. Neste sistema de traços e pontos usados para comunicar à distância, Samuel Morse apercebeu-se que certas letras eram mais comuns do que outras, decidindo assim atribuir uma combinação de traços e pontos mais pequenas às letras mais comuns e combinações maiores às menos frequentes. A compressão de dados segue um processo muito semelhante. No entanto, só em 1948, Claude E. Shannon, através do seu trabalho “A Mathematical Theory of Communication”[2], formalizou os conceitos de compressão de informação em termos teóricos.[1] Este artigo, entre vários conceitos matemáticos complexos, introduziu o conceito de compressão de informação dividida em duas vertentes, compressão lossless (onde não existe perda de informação) e compressão lossy (existe perda de informação durante o processo de compressão) como ilustrado na figura sendo que x=y para lossless e x≠y na lossy. Definiu também que uma compressão lossless iria estar limitada por um limite fundamental, definido pelo rácio de entropia.
Lossless é então obtida através de um método de compressão onde é possível obter exatamente o mesmo conjunto de informação após descompressão, pois é um método não destrutivo. Contrastante com este método, a compressão Lossy é um método destrutivo, impossibilitando reverter
Assim, ao longo dos anos, foram várias as empresas e cientistas que investiram muito no desenvolvimento de algoritmos de compressão para que hoje esteja presente em praticamente todos os aspetos da vida do ser humano, uma vez que muitos dos formatos mais comuns e genéricos do dia-a-dia são baseados em formas de compressão, desde as imagens, aos vídeos, passando pelos ficheiros “zipados”.[3]
“I have made these letters longer than usual because I lack the time to make it shorter”
- Blaise Pascal
Porquê compressão Lossless?
A necessidade de existirem métodos de compressão que consigam garantir a integridade dos dados é de elevada importância, pois por vezes, uma pequena diferença numa letra pode alterar substancialmente o significado de uma frase. Por exemplo as frases “Os rapazes, que comeram marisco, ficaram doentes” e “Os rapazes que comeram marisco ficaram doentes” ficam alteradas apenas pela adição de virgulas. Esta necessidade é exprimida por áreas onde a perda de dados pode originar problemas enormes, como imagem médica, dados de satélites, GPS, etc. [4]
Algoritmos Lossless
Entre os algoritmos de compressão lossless mais famosos, são dignos de nota os LZ77 e LZ78 (também conhecidos como LZ1 e LZ2 respetivamente) não só pela importância cientifica, como pelo facto de serem a base de muitos outros algoritmos importantes. Estes dois algoritmos são codificadores de dicionário, o que significa que estes algoritmos operam através da procura de ligações entre os strings dos dados a comprimir e um set pré-determinado de strings numa estrutura de data - chamada dicionário. A importância destes dois métodos ganha ainda mais relevância, pois foi devido a eles e aos seus pressupostos que mais tarde surgiram os modelos probabilísticos que começaram a criar mapas de probabilidades para serem codificados posteriormente, aumentando drasticamente a capacidade de compressão.[2]
LZ77
O algoritmo da LZ77 atinge a compressão por trocar ocorrências repetidas com referência a uma única cópia existente numa certa posição anterior na corrente de dados. A principal característica deste algoritmo é que usa um método de janela deslizante. Esta janela vai acompanhando a leitura dos dados de input e está dividida em duas partes. A primeira parte é o bloco anterior ao caracter que está a ser lido – cursor - e irá funcionar como dicionário. A segunda parte é o bloco a seguir ao cursor, sendo que este também faz parte do bloco (lookahead buffer). Estes dois blocos são de comprimento fixo e embutidos no algoritmo. Ele é executado da seguinte forma:[5] [6]
- Encontrar o maior match entre uma string que começa no cursor e está completamente embutida no lookahead buffer e uma string que começa no dicionário;
- Devolve um valor triplo (p, n, c) onde p é a posição da ocorrência na janela, n é o comprimento do match e c o caracter após o match;
- Mover o cursor n +1 caracteres para a frente.
No exemplo da imagem, onde o dicionário tem comprimento de 6 (negrito) e o lookahead de 4 (sublinhado) e a posição do cursor dentro do quadrado. A posição p pode ser 0, sendo que significa que não tem match, sendo 1 o primeiro caracter do dicionário (direita para esquerda). Caso encontre strings com tamanhos iguais, guarda o último por questões de performance.
Para a descodificação, basta seguir as posições ao contrário e reconstruir. Um caso particular está na imagem no passo 3, em que n>p. O string a copiar está presente no lookahead buffer e, portanto, ao descodificar ainda não foi construído. O algoritmo corrige este problema repetindo o elemento até preencher n posições.
LZ78
O algoritmo LZ78 é mais conservador na adição de strings ao dicionário e atualmente a variante Lempel-Ziv-Welch (LZW) é a mais comum, dai ser a estudada neste trabalho. O primeiro passo deste algoritmo é formar o dicionário com um tamanho determinado pela memória disponível. Se forem 8 bits, vai-se construir com as 255 primeiras entradas já ocupadas, sendo aumentado ao longo da leitura/codificação e pode ser traduzido com a seguinte interface:[5]
- C’’ = AddDict (C, x) cria uma nova entrada no dicionário por aumentar uma entrada no dicionário existente pelo índex C com o byte x. Retorna novo índex
- C’’ = GetIndex (C, x) retorna o índex de uma string por extensão de uma string correspondente ao índex C com o byte x. Se a entrada n existir, retorna -1
- W = GetString (C) retorna a string W correspondente ao índex C
- Flag = IndexInDict? (C) retorna verdadeiro se o índex C está no dicionário e falso caso contrário.
Para a compressão de “abcabca”, ele inicia a criação do dicionário e vai procurar por “a” que já existe. Como “a” já existe, vai procurar “ab” que não existe e por isso vai criar uma nova entrada no dicionário. Após esta criação vai procurar pelo segundo elemento que é o “b” que também vai existir no dicionário e por isso vai procurar “bc” que não vai existir no dicionário. Assim sendo irá criar uma nova entrada. O mesmo acontece para o “c” e “ca”. No entanto, quando procura de novo “a” após criar o “ca”, vai procurar “ab” que também existe e por isso, irá procurar “abc” que não irá existir e, por conseguinte, criar uma nova entrada.,
Para a descodificação, o algoritmo vai procurar as entradas no dicionário e devolve a string equivalente.[5]
Burrows-wheeler
Este algoritmo, desenvolvido por Michael Burrows e David Wheeler em 1943, é dos grandes algoritmos mais recentes e dos que consegue maiores ganhos de compressão, sendo também muito genérico, resulta muito bem em imagens, sons e texto. O funcionamento deste algoritmo é um pouco diferente dos referidos até agora que analisam o código a comprimir do início como um todo. Este método aborda os dados a comprimir dividido em blocos separados e codifica-os separadamente. A principal ideia por detrás deste algoritmo passa por transformar uma string S com n símbolos numa string L que satisfaça as seguintes condições:[5]
- Cada região de L terá tendencialmente uma concentração de poucos símbolos. Ou seja, se encontrarmos um certo símbolo em L, deveremos encontrar outras instâncias do mesmo por perto. Assim este string poderá ser eficientemente comprimido com outros métodos como move-to-front, RLE ou os já vistos anteriormente. De notar que este método só se torna eficaz a partir de valores elevados de n.
- A possibilidade de reconstruir S a partir de L.
As possibilidades de permutações de símbolos são fatoriais, por isso as possibilidades são enormes, mesmo em casos de poucos símbolos, o que torna vital a escolha adequada das permutações a realizar.
Assim sendo, este método irá começar por criar uma matriz de “n x n” em que n é o tamanho do bloco a ser comprimido, sendo que a primeira linha é o texto original e a seguinte sofre uma translação/shift para a esquerda uma posição, incrementando a translação por 1 a cada linha até termos a translação até n-1. Após isto, ordena-se a matriz por ordem alfabética. Desta matriz retiramos a última coluna (que irá sempre preencher o requisito 1) e guardamos a valor da linha original para poder descodificar. A última coluna e a localização da linha original é então enviado para o codificador.
Para a descodificação, após reconstruir a coluna escolhida para a compressão suplementar, conseguimos facilmente criar a primeira coluna (devido à ordenação léxica). A primeira e última coluna juntas dão-nos a informação necessária para reconstruir pois temos todos os pares de caracteres e a sua sequência. Esta informação permite construir um vetor para as seguintes colunas e a informação guardada da linha original permite reconstruir tudo.
PPM
Não sendo um algoritmo de compressão propriamente dito, mas antes um algoritmo de previsão, o PPM (prediction by partial matching) é usado, entre outras coisas, para fins de compressão de dados. O conceito é elegantemente simples, tendo, no entanto, implementações bem complexas. O algoritmo consegue retornar a probabilidade de distribuição do próximo símbolo a ser codificado, tendo em conta os dados anteriores, semelhante ao formato do dicionário da LZ77, aqui chamada de contexto.[7] Comparando com a língua portuguesa, sabemos que a letra “u” é pouco comum, mas é extremamente comum que apareça depois de um “q”. O mesmo acontece ao contrário: uma consoante a seguir a um “q” é extremamente improvável (para não dizer impossível) na língua portuguesa. Estes casos são muito simples com diferenças de probabilidades enormes, mas a capacidade deste algoritmo passa por detetar tendências mais suaves nos conjuntos de 1 e 0. No entanto, o uso de contextos grandes iria requerer um grande número de cálculos e capacidade de armazenamento das probabilidades condicionais calculadas, o que poderia comprometer o uso do algoritmo. Para fazer face a esta dificuldade, o PPM executa este procedimento faseadamente ao longo da leitura.[7] [3]
O PPM é chamado um modelo de contexto adaptativo porque usa o contexto exatamente precedente ao caracter a codificar e não uma tabela fixa. Ele começa por analisar o contexto C precedente ao caracter S de ordem n (ou tamanho de n caracteres). Caso não encontre no conjunto de dados já processado um contexto C seguido de caracter S, ele assume probabilidade de 0 e recomeça com um contexto de tamanho n-1. Quando a probabilidade é maior que 0, envia para o codificador o símbolo S com probabilidade P.[3] Como um exemplo de compressão de texto, suponhamos que o algoritmo está a analisar um contexto de ordem 3 “dos” que apareceu 27 vezes no passado e 11 vezes foi seguido por um espaço, 9 vezes por uma “s”, 6 vezes por um “e” e 1 vez por um “i”. Se o símbolo a codificar for um espaço, é enviado para o codificador aritmético com uma probabilidade de 11/27 e as probabilidades são atualizadas para 12/28, 9/28, 6/28 e 1/28. Se o símbolo fosse diferente destes (por exemplo um “p”) passaríamos para a ordem 2 (“os”), 1 (“s”), 0 que são as vezes que simplesmente apareceu um ”p” no passado e se mesmo assim nunca tivesse aparecido um “p”, passaríamos para contexto -1 e seria codificado com 1/(tamanho do alfabeto). Ordem -1 é muito comum no início da codificação.[3] Para se conseguir descodificar, a alteração da ordem do contexto tem de ficar contabilizada e perfeitamente indicada, pois descodificador não sabe qual é o caracter seguinte. Isto é feito através de um escape symbol para o descodificador saber que tem de reduzir a ordem do contexto. Assim no caso referido em cima, quando o codificador chega a um contexto de ordem -1, vindo de um de ordem 3, deve antes ter codificado 4 escape symbols antes.
Seguindo o exemplo da figura, assumindo que “assanissimassa” já foi codificado e está-se a utilizar uma ordem de contexto 2 (“sa” portanto), podem acontecer 1 de 4 alternativas baseadas no caracter a seguir:[3]
- Caso fosse “n”, o algoritmo já tinha encontrado “sa” seguido por um “n” e, portanto, iria enviar a probabilidade (1/2)
- Caso fosse “s”, o algoritmo nunca viu “sa” seguido de um “s”, e iria, portanto, descer um nível de ordem de contexto que passaria a “a” e enviaria para o codificador um escape symbol com probabilidade (1/2). Como o codificador já viu um “a” seguido de um “s”, envia com a probabilidade associada (2/5)
- Caso fosse “m”, o algoritmo não iria encontrar match nos contextos de ordem 2 nem 1 por isso passaria para o contexto 0 (enviando dois escape symbols) e mandaria o “m” sozinho e a sua probabilidade (1/19)
- Finalmente temos o caso de ser por exemplo um “d” que o algoritmo nunca viu. Por isso nenhuma das ordens de contexto anteriores iria encontrar match e, portanto, iriam ser codificados 3 escape symbols e enviaria o “m” com a probabilidade de 1/28 (todo o alfabeto/hipóteses)[3]
PAQ e Content-mixing
O PAQ é um algoritmo open-source veio trazer alguma disrupção ao mundo da compressão. Este algoritmo de alta-performance baseado em context-mixing está atualmente no topo dos rankings de compressão, apesar de ter um custo elevado de memória e tempo (quem tem vindo a ser combatida). Mas a grande revolução está associada ao facto de ser open-source e permitir muitas versões, subversões, derivações e spin-offs. O uso de context-mixing tem sido o principal objeto de intervenção e desenvolvimento nos últimos tempos, principalmente devido à aplicação de conceitos experimentais de machine-learning. De certa forma este formato teve origem através do PPM e do Burrows-Wheeler , uma vez que é baseado em distribuição algorítmica. No entanto existem duas grandes diferenças:[8] [9]
- O contexto passa a ser uma função complexa dos dados já vistos;
- Ao invés de um único modelo previsor, existem vários modelos.
O PAQ consegue ultrapassar algumas das limitações do PPM, não requisitando que os contextos sejam contíguos. Context-mixing entra neste modelo na medida em que o PAQ não usa apenas um modelo de probabilidades, mas vários que posteriormente cruza e atribui pesos diferentes. Os principais modelos de contexto são:[8] [3]
- n-grams; em que é baseado nos últimos n bytes antes do símbolo a prever (tal como o PPM);
- whole-word n-grams, ignorando letras maiúsculas e caracteres não alfabéticos (útil em texto);
- Contextos “sparse” que apenas conta o segundo e quarto byte antes do símbolo a prever (útil em alguns formatos binários);
- Contextos analógicos, consistindo em bits de ordem elevada 8-16 bit (útil em multimédia);
- Modelos especializados que são executados quando um certo formato de ficheiro é detetado.
A união dos resultados destes modelos irá originar a probabilidade a codificar para o caracter. A probabilidade é ponderada tendo em conta os pesos dos modelos. A título de exemplo, do PAQ1 ao PAQ3, as várias probabilidades eram combinadas por somatório ponderado, sendo que era atribuído um peso superior aos contextos mais longos. Do PAQ4 ao 6, eram atribuídos maiores pesos aos contextos mais exatos e finalmente a partir do PAQ7, as probabilidades eram atribuídas usando redes neurais. [8] [3]
Formatos de ficheiros
Entre os formatos de compressão mais conhecidos, o que é sem duvida mais conhecido é o “.zip”. Este formato está amplamente difundido a nível mundial pela sua capacidade de compressão, rapidez e compatibilidade. Este formato foi criado por Phil Katz em 1989 e consegue utilizar vários algoritmos, mas usa essencialmente DEFLATE que é baseado no LZ77 e que também foi desenvolvido por Katz. Consegue comprimir até 16 exabytes de ficheiros. 9 O formato .rar também tem tido alguma popularidade pelo publico geral e é baseado nos algoritmos de Lempel-Ziv e PPM. Foi criado por Eugene Roshal, sendo que é dai que deriva o seu nome – Roshal ARchive. Os programas usados são o RAR e o WinRAR que oferecem completo suporte para .rar e .zip. Consegue também descomprimir um conjunto de outros formatos, mas não comprimir. Consegue comprimir até 8,6 biliões de gigabytes (ou qualquer coisa como 7.8 zettabytes).[3]
Benchmark
Para se perceber de que maneira se fazem as comparações entre algoritmos, é preciso perceber alguns conceitos que serão comuns a todos.
São eles rácio de compressão, fator de compressão e ganhos de compressão.
O rácio é uma fórmula simples e intuitiva:[3]
Rácio de compressão=(Tamanho do output) / (Tamanho do input)
Esta também é reconhecida por bit per bit, porque irá traduzir na quantidade de bits necessários para traduzir um bit do input. A expressão 100x (1- rácio de compressão) é usada como intermutável com o rácio, embora neste caso um valor de 80% indicará que o resultado ocupa 20% do original. O fator de compressão é o rácio elevado a -1 ou:[3]
Fator de compressão=(Tamanho do input)/(Tamanho do output)
Neste momento no topo em termos de capacidade de compressão estão os algoritmos baseados em context-mixing como nanozip, modificações da PAQ e do PPM que já conseguem valores de compressão ao nível do bit por byte, como se pode verificar em sites especializados nestes testes como o imagecompression e o squeezechart.
Atualmente existe um concurso chamado de “Hutter Prize”, iniciado em 2006 por Marcus Hutter, onde a candidatura é aberta a toda a gente e oferece 500 euros por cada 1% de compressão adicional sobre o atual vencedor. O ficheiro a comprimir é o enwik8 que se baseia nos primeiros 100 000 000 caracteres da wikipedia em inglês[10]. Os últimos 3 algoritmos vencedores foram da autoria de Alexander Rhatushnyak com versões do PAQ.[10]
Compressão de dados em Saúde
A imagem médica tem sido um dos campos de maior desenvolvimento no que diz respeito a aplicações biomédicas. Por conseguinte, a compressão sem perdas surge como fundamental nesta área, pois toda a informação contida num pixel é de extrema importância. Contudo, é essencial que esse processo possua uma elevada taxa de compressão bem como a capacidade de descodificar os dados comprimidos em várias resoluções. Esses dados são armazenados em sistemas de arquivo computorizados como PACS (Picture Archiving and Communication System) e DICOM (Digital Imaging and Communications in Medicine), seguindo sempre as normas internacionais HL7 para a troca de informação em forma de texto.[11][12][13] Estes desenvolvimentos levaram a um aumento exponencial da quantidade de dados médicos, pois a obtenção de imagens cada vez mais frequente e o seu tamanho é cada vez maior (como visto na imagem em baixo). Este aumento tornou imprescindível o desenvolvimento de técnicas para armazenamento, gestão e proteção das mesmas, pois cada vez mais as imagens médicas são armazenadas digitalmente, principalmente na área da radiologia.[14] [12]
Torna-se assim necessário arranjar métodos eficazes para a gestão desta quantidade de informação sem ocupar espaços digitais gigantescos.[15] Uma redução na quantidade de espaço necessário para o armazenamento de dados traz muitas vantagens como a redução da largura de banda, do custo e do tempo necessários para a transmissão de dados, potencializando análises mais rápidas e fáceis à distância. [12]
Mecanismos de compressão lossless de imagens Raio-x
Desde 1895 (ano da sua descoberta) até à atualidade, as imagens obtidas por radiação x continuam a ser uma ferramenta importante no diagnóstico médico. Contudo, a telemedicina trouxe a necessidade de armazenar e transmitir eficientemente essas imagens. O método que de seguida se descreve elimina os dados que não pertencem à região de interesse na imagem de raio-x. Os pixéis de fundo não contém informações médicas relevantes e, portanto, serão removidos. A região de interesse será separada dos pixéis de fundo e posteriormente comprimida por compressão lossless, promovendo assim uma redução do tamanho da imagem bipartido, pela remoção de informação e pela compressão em si . A segmentação seguida de compressão torna-se difícil de atingir pelo facto de existirem regiões cuja intensidade não é uniforme entre o osso e partes moles nas imagens de radiologia convencional. Métodos de segmentação baseados em bordas, como Canny e Sobel, quando aplicados a imagens de raio-x não apresentaram uma eficaz segmentação. Embora não haja um método 100% fiável na extração da região de interesse nas imagens de raio-x, Kazeminia e seus colaboradores desenvolveram um método para extração da região de interesse que se baseia na análise de distribuição dos pixéis de fundo nas imagens. Primeiramente é encontrada a intensidade que separa a região de interesse da região de não interesse, para depois ser atribuído o mesmo valor à intensidade dos pixéis dessa região de não interesse. [16] [15]
O ruído inevitavelmente existente nas imagens de raio-x e que influencia as regiões de interesse pode ser removido com recurso a filtros Gaussianos. A deteção da região de interesse é feita com recurso ao histograma da imagem. Os valores abaixo da concavidade negativa do histograma são separados dos restantes que correspondem à região de interesse (representado pela seta vermelha no gráfico da figura). É aplicada uma máscara binária, transformando em 0 todos os pixéis abaixo desse limiar da concavidade negativa do histograma (isto porque esses pixéis não têm dados importantes). Os píxeis acima desse limiar assumem o valor 1. [16] [15]
Para comprimir os dados da máscara binária referida constituída por 0 e 1, é usada a técnica de codificação run-lenght (RLE), útil quando há sequências longas de carateres iguais. Numa primeira fase, RLE converte a imagem numa sequência e depois faz o cálculo do número de valores semelhantes até encontrar um valor diferente. Dadas as sequências longas de 0 e 1, a técnica RLE torna-se eficiente nesta máscara binária. [16] 18 Pixéis vizinhos nas regiões de interesse têm intensidades semelhantes, logo pode concluir-se que há redundância espacial. Assim sendo, essa redundância espacial pode ser convertida em redundância estatística pelo preditor ALCM (activity level classification model), que tem sido implementado na compressão de imagens 3D obtidas por ressonância magnética. [16] O valor do pixel atual no ALCM é predito por uma combinação linear de alguns dos píxeis vizinhos que já estão processados. Os pesos desta combinação linear são calculados à medida que a codificação prossegue. O mesmo peso é inicialmente atribuído a todos os píxeis envolvidos. Após a predição ser realizada, os pesos poderiam mudar da seguinte maneira: Se o valor previsto fosse menor que o valor real do pixel então 1/256 é subtraído do peso do maior pixel da vizinhança e adicionado ao peso do menor. Se o valor predito fosse maior do que o pixel real, então o peso do pixel da vizinhança maior é aumentado em 1/256 e o peso do menor é reduzido. [16] Após aplicação do algoritmo em MatLab 2013 e testado em 60 imagens de raio-x, o método de compressão descrito tem a taxa mais baixa de bits mesmo quando comparada com métodos como SPIHT, JPEG-LS e APT. [16] [17]
Compressão em mamografia
À semelhança do que foi referido para as imagens ósseas obtidas por raio-x, também na mamografia existem grandes benefícios com o armazenamento digital eficaz das imagens e da fácil transmissão das mesmas. Para se ter uma ideia do espaço necessário, o estudo standard da incidência oblíqua médio-lateral e crânio-caudal podem ocupar 120 Megabytes em disco. No final de um dia, o espaço requerido para as mamografias realizadas é demasiado, sendo de extrema utilidade a compressão sem perda de dados.[18] Este método irá decompor a imagem mamográfica em planos de bits para de seguida os comprimir separadamente pelo PPM adaptado ao alfabeto binário para os requisitos computacionais serem ainda menores. A decomposição em plano de bits decompõe uma imagem S de n bits por pixel (ou seja, 2n níveis de cinza) em n imagens binárias, ou planos de bits, s0, s1, …, sn-1. Um pixel no plano si equivale ao i-ésimo bit do pixel nas mesmas coordenadas em S. A figura seguinte ilustra, a título de exemplo, essa decomposição em três planos.[18] [19]
Para separar a região da mama do background foi efetuada a segmentação por limiarização. Seja X um valor escolhido com as características do background da mama. Os píxeis com valor maior que X são classificados como mama, os restantes correspondem ao background.[18]
Para permitir a descompressão correta dos dados, uma imagem binária será adicionada ao arquivo comprimido: de valor 1 indicará a região da mama e de valor 0 indicará o background.[18] A representação binária usada foi o código Gray onde dois números sucessivos se distinguem por um bit. Por norma, nas imagens médicas dois valores consecutivos não variam significativamente devido à natureza contínua dos sinais originais e, por tal razão, a compressão por planos de bits é mais eficaz. Essa variação é reduzida com o código Gray: pela análise da tabela observa-se que na transição 3-4 no código convencional binário todos os bits alteraram enquanto no código Gray só o primeiro sofreu alteração.[18]
Este conteúdo em vídeo
Caso pretenda a visualização deste conteúdo em vídeo clique aqui.
Referências Bibliográficas
- ↑ Nelson, M. (1991) The Data Compression Book. IDG Books Worldwide, Inc., Cambridge
- ↑ Shannon, C., & Weaver, W. (1949) The Mathematical Theory of Communication. Urbana: University of Illinois Press
- ↑ 3,00 3,01 3,02 3,03 3,04 3,05 3,06 3,07 3,08 3,09 3,10 Salomon, D. & Motta, G. (2010) Handbook of Data Compression Fifth Edition. Springer-Verlag London, California
- ↑ Sayood, K. (2006) Introduction to Data Compression Third Edition. Morgan Kaufmann, Nebraska
- ↑ 5,0 5,1 5,2 5,3 Blelloch, G. (2013) Introduction to Data Compression. Carnegie Mellon University
- ↑ Ziv, J., & Lempel, A. (1977). A universal algorithm for sequential data compression. IEEE Transactions on Information Theory
- ↑ 7,0 7,1 Cleary, J., & Witten, I. (1984). Data Compression Using Adaptive Coding and Partial String Matching. IEEE Transactions on Communications
- ↑ 8,0 8,1 8,2 Blaszczy, K. (2012) PAQ compression algorithm. RWTH Aachen University
- ↑ Mahoney, M. (2005) Adaptive Weighing of Context Models for Lossless Data Compression. Florida Tech. Technical Report CS-2005-16, Florida
- ↑ 10,0 10,1 http://prize.hutter1.net/ (acedido dia 05/04/2017)
- ↑ Badshah, G., Liew, S., Zain, J. M., Hisham, S. I., & Zehra, A. (2015). Importance of Watermark Lossless Compression in Digital Medical Image Watermarking. Research Journal of Recent Sciences, 4(3), 75–79.
- ↑ 12,0 12,1 12,2 Janet, J., Mohandass, D., & Meenalosini, S. (2011). Lossless Compression Techniques for Medical Images in Telemedicine. Advances in Telemedicine:Technologies, Enabling Factors and Scenarios, 111–131.
- ↑ Anusuya, V., Raghavan, V. S., & Kavitha, G. (2014). Lossless Compression on MRI Images Using SWT. Journal of Digital Imaging, 27(5), 594–600. https://doi.org/10.1007/s10278-014-9697-9
- ↑ 14,0 14,1 Scholl et al., Challenges of medical image processing. Comput Sci Res Dev (2011) 26: 5–13
- ↑ 15,0 15,1 15,2 Gonzalez, R. C. & Woods, R. E. “Digital Image Processing”. Addison-Wesley Publishing Company, 1992.
- ↑ 16,0 16,1 16,2 16,3 16,4 16,5 16,6 Kazeminia, S., Karimi, N., Soroushmehr, S. M. R., Samavi, S., Derksen, H., & Najarian, K. (2015). Region of interest extraction for lossless compression of bone X-ray images. Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, 2015–November, 3061–3064. https://doi.org/10.1109/EMBC.2015.7319038
- ↑ Rema, N. R., Oommen, B. A., & Mythili, P. (2015). Image compression using SPIHT with modified spatial orientation trees. Procedia Computer Science, 46(Icict 2014), 1732–1738. https://doi.org/10.1016/j.procs.2015.02.121
- ↑ 18,0 18,1 18,2 18,3 18,4 Marques, J. R. T., Honório, T. C. S., Kees, J., Souza, A. R. C. De, & Batista, L. V. (2007). Compressão sem Perdas de Imagens Mamográficas Utilizando Código Gray e Algoritmo PPM, 1216–1217.
- ↑ Zhang, Y., & Adjeroh, D. A. (2008). Prediction by partial approximate matching for lossless image compression. IEEE Transactions on Image Processing, 17(6), 924–935. https://doi.org/10.1109/TIP.2008.920772


![Volumes de dados para diagnóstico médico[14]](/images/3/30/L-compressao.PNG)
![Imagem original de raio-x b) Extração da região de interesse com o Watershed c) Segmentação da imagem com crescimento de região d) Extração da região de interesse com o método thresholding e) Deteção de bordas com o método Canny f) Suavização da imagem com filtro Gaussiano [16]](/images/2/2f/G-extrac.png)