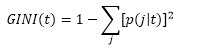Modelo Preditivo

Extração de Conhecimento de Dados

“We study the past to understand the present; we understand the present to guide the future.” - William Lund

Introdução

A Extração de Conhecimento de Dados, muitas das vezes denominada de Data Mining, pode ter diferentes definições dependendo da perspectiva.

Numa perspectiva de negócio o Data Mining é definido como o processo de identificação de relacionamentos e padrões existentes numa base de dados. Pode ainda ser definido como a extração de informação útil para o negocio a partir de grandes bases de dados.

Numa perspectiva mais funcional é a procura de informação importante em grandes volumes de dados, resultado da cooperação de esforços humanos e de computadores. Os humanos desenham as bases de dados, descrevem problemas e estabelecem objetivos. Os computadores esmiúçam os dados, procurando padrões que correspondam aos objetivos.

Numa perspectiva mais acadêmica será a extração implícita, não trivial de conhecimentos úteis e padrões válidos, previamente desconhecidos, dos dados.

Modelo Preditivo

A análise preditiva é o uso de dados e algoritmos para identificar a probabilidade de resultados futuros com base em dados históricos. Os modelos preditivos utilizam os resultados conhecidos para desenvolver e treinar um modelo que possa ser usado para prever valores para dados diferentes ou novos, usando para isso um algoritmo preditivo de Data Mining.

Um algoritmo preditivo é uma função que, dado um conjunto de exemplos rotulados, constrói um estimador. Se o domínio dos rótulos for um conjunto de valores nominais, estamos perante um problema de classificação, e o estimador criado é uma classificador. Se o domínio for um conjunto infinito e ordenado de valores, estamos perante um problema de regressão e é criado um regressor.

Um estimador (classificador ou regressor) é uma função que atribui a uma das classes, ou um valor real, a um exemplo não rotulado.

Classificação: em que assume valores num conjunto discreto não ordenado.

Regressão: em que assume valores num conjunto infinito e ordenado.

O objetivo é encontrar uma fronteira de decisão que separe os exemplos de uma classe dos exemplos da outra classe.

Diferentes algoritmos de Data Mining podem encontrar diferentes fronteiras de decisão.

---

Métodos baseados em Procura

A aprendizagem automática passa também pela procura num conjunto de possíveis opções. A esta procura está associado também um viés, o viés de procura. Este viés representa o atrito e erro associado à procura de hipóteses num espaço de soluções.

Árvores de decisão e Regressão

Um modelo de árvore de decisão é utilizado para resolver problemas com base na classificação. Uma árvore de decisão utiliza a estratégia de “dividir para conquistar”, isto é, um problema de procura deverá ser simplificado dividindo o problema “major” em menores problemas. A esses problemas menores, a mesma estratégia é utilizada e têm o nome de subproblemas. As soluções aos subproblemas obtidas são então compactadas de forma a gerar uma solução para o problema original ou “major”.

Um modelo de árvore de regressão é utilizado para resolver problemas com base na regressão. Este modelo utiliza a mesma estratégia de dividir que a árvore de decisão, mas neste caso para valores contínuos.

No caso destes valores contínuos, existem duas formar de se tratar da divisão: discretização para formar um atributo ordinal categórico (estático, em que se discretiza uma vez no início ou dinâmico em que os intervalos podem ser determinados por tamanho, frequência ou clustering) ou decisão binária (considera todas as divisões possíveis e considera a melhor).

Alguns dos algoritmos baseados em árvores de decisão e regressão são: ID3 (Quinlan, 1979), ASSISTANT (Cestnik et al., 1987), CART (Breiman et al., 1984), C4.5 (Quinlan, 1993). O algoritmo mais utilizado para a classificação é o CART, seguido do seu competidor C4.5.

Tanto uma árvore de decisão como uma árvore de regressão são um grafo acíclico direcionado constituído por nós de divisão com dois ou mais sucessores, ou nós folha.

Um nó de divisão é um teste condicional baseado nos valores do atributo. Um teste condicional é por exemplo:

- Temperatura > 30 ºC;

- Sexo ϵ {Masculino, feminino};

-

Um nó folha é uma função. Em problemas de classificação, a constante que minimiza a função de custo é 0-1 e é a moda. Em problemas de regressão, a constante é a média.

Ganho de Informação

O ganho de informação está subjacente ao conceito de entropia. A entropia é uma medição da aleatoriedade de uma variável aleatória, cuja função é:

Neste caso, p seria a probabilidade de observar A=0 e p-1 a probabilidade de observar A=1. No caso das árvores de decisão, a entropia representa a aleatoriedade do atributo alvo, ou seja, a dificuldade para predizer determinado atributo. O índice Gini é uma regra de ganho de informação usado no CART.Este índice de Gini pode ser considerado uma medida de impureza ou como método de divisão na árvore. Na divisão de atributos categóricos, o índice de Gini pode realizar um multi-way split ou um binary split. Este índice é representado pela seguinte fórmula:

Estratégias de Poda

A poda é um passo essencial na construção de uma árvore de decisão ou regressão pois é esta que irá reduzir ao máximo o ruído da informação. O ruído da informação pode provocar que a árvore classifique objetos de um modo não confiável e o tamanho das árvores tende a ser muito extenso quando o ruído existe. A poda é importante então para diminuir o erro devido à variância do classificador.

A poda pode ser classificada então em pré-poda, em que se para a construção da árvore quando algum dos critérios pré estabelecidos é satisfeito; e pós-poda, em que tal como o nome indica, a construção é concluída e só após é feita a poda.

Vantagens e Desvantagens

Vantagens:

1. Flexibilidade – Sendo um método não paramétrico, não existe uma distribuição dos dados, estes são dispostos em espaços e cada espaço é aproximado com recurso a muitos modelos.
2. Robustez – A estrutura das árvores não varia em por exemplo árvores univariadas. Não sofrem transformações.
3. Seleção de atributos – Durante o processo de construção, os atributos tendem a ser robustos e atributos mais irrelevantes e redundantes são fragilizados.
4. Interpretabilidade – Interpretando decisões mais simples e locais, podem-se realizar decisões mais complexas e globais.
5. Eficiência – Como o algoritmo de um árvore de decisão é top-down usando uma estratégia de dividir, esta torna-se bastante eficiente.

Desvantagens:

1. Replicação – Refere-se à duplicação de testes em diferentes ramos da árvore.
2. Valores ausentes – Se um valor de atributo é desconhecido, não poderá ser continuado o ramo.
3. Atributos contínuos – A ordenação de cada atributo contínuo estima-se que consuma 70% do tempo necessário para induzir uma árvore de decisão.
4. Instabilidade – Breiman (1996) e Kohavi e Kunz (1997) apontaram que variações no conjunto de treino podem produzir grande variações na árvore final. Mudando um nó, todas as sub-árvores abaixo desse nó mudam.

Figura 1. Representação de uma árvore de decisão efetuada no Rapidminer com dados dos sobreviventes do “Titanic”.

O UCI Machine Learning Repository constitui uma excelente fonte de bases de dados que poderão ser utilizadas de forma gratuita para a aprendizagem da utilização de softwares como rapidminer e weka.

Regras de Decisão

Uma regra de decisão tem a forma de Se X Então Y (if X then Y), em que X pode ser uma ou várias condições. Cada condição relaciona um atributo com valores do seu domínio, múltiplas condições podem-se juntar com um dos operadores: e ou ou. A relação pode ser uma do conjunto .

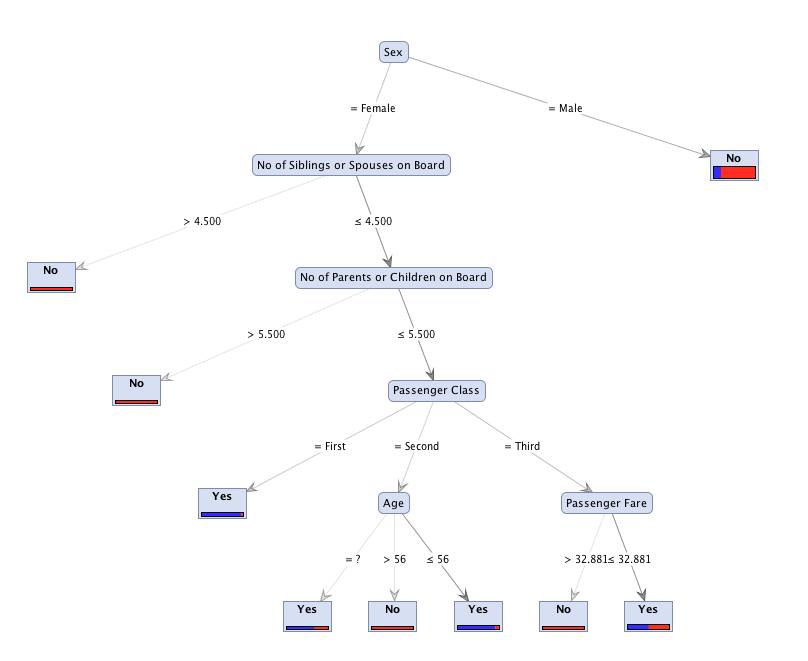
Um exemplo de uma regra de decisão, com base na figura 1, é if Sex = Male then No

Árvores de Decisão podem ser representadas como conjuntos de regras de decisão, que são escritas considerando o caminho do nó raiz até uma folha da árvore, com o intuito de facilitar a leitura e a compreensão. É portanto possível derivar regras de uma Árvore de Decisão.

Uma regra pode ser compreendida sem que haja a necessidade de referenciar-se a outras.

Algoritmo de OneR

O algoritmo OneR (One Rule), proposto por Holte (1993) gera regras baseadas num único atributo. O OneR considera para cada atributo, uma regra por cada valor desse atributo, para cada atributo é calculada a taxa de erro (proporção de erros feitos sobre todo o conjunto de exemplos), e o atributo com menos taxa de erro é o escolhido.

Nas tabelas seguintes podemos ver um exemplo prático da aplicação do algoritmo OneR.

Outlook	Temperature	Humidity	Windy	Play
sunny	hot	high	false	no
sunny	hot	high	true	no
overcast	hot	high	false	yes
rainy	mild	high	false	yes
rainy	cool	normal	false	yes
rainy	cool	normal	true	no
overcast	cool	normal	true	yes
sunny	mild	high	false	no
sunny	cool	normal	false	yes
rainy	mild	normal	false	yes
sunny	mild	normal	true	yes
overcast	mild	high	true	yes
overcast	hot	normal	false	yes
rainy	mild	high	true	no

Attribute	Rules	Errors	Total errors
outlook	sunny → no overcast → yes rainy → yes	2/5 0/4 2/5	4/14
temperature	hot → no mild → yes cool → yes	2/4 2/6 1/4	5/14
humidity	high → no normal → yes	3/7 1/7	4/14
windy	false → yes true → no	2/8 3/5	5/14

outlook

sunny → no overcast → yes rainy → yes

Algoritmo de Cobertura

O algoritmo de cobertura, um dos mais divulgados na aprendizagem de regras a partir de exemplos, define o processo de aprendizagem como um processo de procura. O algoritmo procura regras da forma: Se atributoA = valorX e atributoB = valorY e … então ClasseZ.

De seguida é apresentado o algoritmo de cobertura

• Entrada: Um conjunto de treino D = {(xi, yi), i = 1, ..., n }
• Saída: Um conjunto de regras: Regras
• Regras ← {};
• Seja Y o conjunto das classes em D;
• para cada yi ∈ Y faça
  • repita
    • Regra = Aprende_Regra(D, yi);
    • Regras ← Regras ∪ {Regra};
    • D ← Remove exemplos cobertos pela Regra em D;
  • até não haver exemplos de yi;
• fim
• Retorna: Regras;

Têm sido usadas duas estratégias básicas de procura de regras. Uma baseada numa estratégia top-down que começa na regra mais geral tornando-se depois mais específica acrescentando condições. A segunda começa pela regra mais específica e vai removendo condições tornando-se mais generalizada, é uma estratégia bottom-up e orientada pelos dados.

Uma regra torna-se mais específica quando é acrescentada uma condição diminuindo o número de exemplos cobertos pela regra, por outro lado, torna-se mais geral quando se remove uma condição aumentando o número de exemplos cobertos pela regra.

Algoritmo top-down

• Entrada: Um conjunto de treino D = {(xi, yi), i = 1, ..., n }
• y: classe da regra
• Saída: Uma regra de classificação: Regra
• Seja Avs o conjunto de atributo_valores em D;
• Regra ← {};
• v ← Avalia(Regra, D, y);
• melhor ← v;
• continua ← Verdadeiro;
• enquanto continua faça
  • continua ← Falso;
  • para cada avi ∈ Avs faça
    • val ← Avalia(Regra ∪ avi , D, y);
    • se val < melhor então
      • melhor ← val;
      • Cond ← avi;
      • continua ← Verdadeiro;
    • fim
    • fim
  • se continua então
    • Regra ← Regra ∪ Cond;
  • fim
• fim
• Retorna: Regra;

Algoritmo Bottom-up

• Entrada: Um conjunto de treino D = {(xi, yi), i = 1, ..., n }
• y: classe da regra
• Saída: Uma regra de classificação: Regra
• Escolhe, aleatóriamente, um exemplo da classe y em D;
• Seja Regra o conjunto de atributo_valor desse exemplo;
• v ← Avalia(Regra, D, y);
• melhor ← v;
• continua ← Verdadeiro;
• enquanto continua faça
  • continua ← Falso;
  • para cada avi ∈ Regra faça
    • val ← Avalia(Regra \ avi , D, y);
    • se val < melhor então
      • melhor ← val;
      • Cond ← avi;
      • continua ← Verdadeiro;
    • fim
  • fim
  • se continua então
    • Regra ← Regra \ Cond;
  • fim
• fim
• Retorna: Regra;

A diferença fundamental entre os dois algoritmos é que o método top-down gera regras ordenadas pela ordem que são induzidas enquanto o método bottom-up gera um conjunto não ordenado. Esta diferença implica que a aplicação do conjunto de regras a exemplos não classificados seja, no caso do top-down, cada exemplo é classificado pela primeira regra satisfeita, no caso bottom-up, todas as regras satisfeitas são utilizadas para classificar o exemplo, optando pela regra com melhor qualidade.

A qualidade da regra deve ser medida tendo em conta :

• nCover: número de exemplos cobertos pela regra;
• nCorreto: número de exemplos cobertos pela regra que foram corretamente classificados pela regra;
• cobertura: definida como nCover / n;
• taxa de acerto: definida como nCorreto / nCover.

---

Métodos Probabilísticos:

Uma das maneiras de lidar com tarefas preditivas em extração do conhecimento de dados;

Útil quando as informações disponíveis são incompletas ou imprecisas;

Uso de algoritmos baseados no Teorema de Bayes (Métodos Probabilísticos Bayesianos): a probabilidade de um evento A dado um evento B não depende apenas da relação entre A e B, mas também da probabilidade de observar A independentemente de observar B.

Probabilidade de ocorrer o evento A, dado que foi observado o evento B: P(A|B), onde A representa a classe e B o valor observado dos atributos para um exemplo de teste.

Exemplo: P(A) = probabilidade de ocorrência de uma determinada doença; P(B) = probabilidade de resultado num exame de raio X; sendo a variável A não observável e diante da evidência do resultado do exame de raio X, podemos inferir o valor mais provável de A estimando:

Aprendizagem Bayesiana:

Doença
Presente	8%
Ausente	92%

Quantitativa (a probabilidade a priori de observar a doença):

P(Doença = Presente) = 0,08,

P(Doença = Ausente) = 0,92.

Doença
Teste	Presente	Ausente
Positivo	75%	4%
Negativo	25%	96%

Probabilidades condicionais (a partir de experiências passadas na utilização do teste):

P(Teste = Positivo |Doença = Presente) = 0,75,

P(Teste = Negativo |Doença = Ausente) = 0,96.

Qual é o poder preditivo do Teste com respeito à Doença? Se A e B são eventos disjuntos, então ;

Lei da probabilidade total:

Lei da probabilidade condicional:

Dedução:

Já que P(A) = P(A|B) X P(B), então:

P(Teste = Positivo) = P(Teste = Positivo |Doença = Presente) X P(Doença = Presente) + P(Teste = Positivo |Doença = Ausente) X P(Doença = Ausente) = 0,75 X 0,08 + 0,04 X 0,92 = 0,0968.

P(Teste = Negativo) = P(Teste = Negativo |Doença = Presente) X P(Doença = Presente) + P(Teste = Negativo |Doença = Ausente) X P(Doença = Ausente) = 0,25 X 0,08 + 0,96 X 0,92 = 0,9032.

O problema de Inferência e o Teorema de Bayes: a sua aplicabilidade é reduzida devido ao grande número de exemplos necessários para calcular, de forma viável.

O classificador naive Bayes

Um dos classificadores Bayesianos mais populares;

Assume que os valores de atributos são independentes entre si dada a classe;

Todas as probabilidades necessárias para a obtenção do classificador são calculadas a partir dos dados de treino;

Não há a busca explícita por uma hipótese, mas o produto das probabilidades de cada atributo individual (porém é necessário manter um contador para cada classe para o cálculo da probabilidade a priori);

Para o cálculo da probabilidade condicional é necessário distinguir entre atributos nominais e atributos contínuos;

Atributos nominais: conjunto de valores possíveis é um conjunto enumerável – um contador para cada valor de atributo por classe;

Atributos contínuos (número de valores possíveis infinito):

1. Assumimos uma distribuição normal;
2. Discretizar o atributo no pré-processamento (melhores resultados do que assumir distribuição normal):

1. Número de intervalos fixado em um k = mínimo (que pode ou não ser igual a 10) / intervalos do mesmo tamanho;
2. Depois de discretizar um atributo podemos calcular a probabilidade condicional ao utilizar um contador para cada classe e para cada intervalo.

Análise do algoritmo

1. Superfície de decisão linear (naive Bayes num problema de duas classes definidos por atributos booleanos é um hiperplano);
2. As probabilidades exigidas pela equação que determina a probabilidade de um exemplo pertencer à classe em questão podem ser calculadas a partir do conjunto de treino numa única passagem;
3. Processo de construção do modelo bastante eficiente;
4. Fácil de implementar de forma incremental;
5. Bom desempenho numa grande variedade de domínios, incluindo domínios em que há clara dependência entre os atributos;
6. Robusto à presença de ruído e atributos irrelevantes;
7. Teorias aprendidas são fáceis de compreender pelos especialistas do domínio (resume a variabilidade do conjunto de dados em tabelas de contingência);
8. Desempenho do modelo não decresce na presença de atributos irrelevantes;
9. Problema da frequência = 0. Se uma das frequências for igual a zero devemos adicionar 1 a todos os valores da tabela;

Desenvolvimentos (técnicas para melhorar o desempenho do classificador naive Bayes)

1. Langley (1993) = recursivamente constrói uma hierarquia das descrições dos conceitos probabilísticos;
2. Kohavi (1996) = árvore de naive Bayes (algoritmo híbrido que gera uma árvore de decisão univariada regular cujas folhas contêm um classificador naive Bayes;
3. Kononenko (1991) = classificador semi-naive Bayes (combina pares de atributos, fazendo um atributo produto-cruzado);
4. Pazzani (1996) = classificador construtivo, encontrar os melhores atributos do produto cartesiano a partir de atributos nominais existentes;
5. John (1994) = Bayes flexível para atributos contínuos;
6. Gama (2000) = Linear Bayes, distribuição normal multivariada para cada classe (atributos contínuos).

Redes Bayesianas para classificação: Modelos gráficos probabilísticos

Grafo Acíclico Direcionado (DAG) (cujos nós representam variáveis aleatórias e as arestas representam dependências diretas entre as variáveis) + conjunto de tabelas de probabilidade condicional;

Causal; escolha de nós e dependências entre variáveis na rede; probabilidades condicionadas;

Casos em que existe uma relação estatística entre duas variáveis quando uma terceira variável é conhecida (independência condicional entre variáveis);

Obter um equilíbrio entre o número de parâmetros a calcular e a representação de dependências entre variáveis;

Representam a distribuição de probabilidade conjunta de um grupo de variáveis aleatórias num domínio específico;

Utilizada para tarefas de classificação de uma forma relativamente simples;

Uma das variáveis é selecionada como atributo alvo e todas as outras são consideradas como atributos de entrada;

Dado um conjunto de treino a aprendizagem consiste em selecionar o classificador baseado em Redes Bayesianas, isto é, a hipótese que produz a classificação com maior taxa de acerto para dados não conhecidos;

O objetivo é construir um classificador com elevada taxa de acerto preditiva;

---

Métodos baseados em Otimização

Um outro método de aprendizagem automática é o denominado metido de otimização que tem como principal objetivo minimizar (ou maximizar) uma determinada função. Este método baseia-se em duas técnicas de extração de conhecimento de dados que recorrem à optimização de uma função de custo na fase de treino e que são : Redes Neuronais Artificiais (RNA) e Máquinas de Vetores de Suporte (SBM). O nosso estudo incidirá apenas sobre as RNA.

Redes Neuronais Artificiais

O desenvolvimento das redes neuronais artificiais teve como principio a estrutura e funcionamento do sistema nervoso humano de forma a que se pudesse ter uma proximidade de simular a capacidade de aprendizagem do nosso cérebro na realização de tarefas que podem ser consideradas simples tais como pegar num objeto mas que apenas são possíveis devido à complexa estrutura do cérebro humano.

Deve-se a McCulloch e Pitts (1943) o inicio da pesquisa deste tipo de modelos computacionais tendo sido desenvolvido um primeiro modelo matemático denominado de unidades logicas com limiar (LTU em inglês).

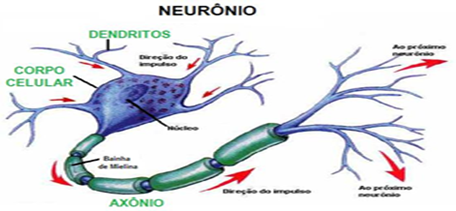
Este modelo tem como base o Neurónio Biológico sendo que este é o principal bloco de construção do nosso cérebro conforme ilustrado na figura 2 abaixo.

Figura 2 - Esquema de um neurónio e da forma como o impulso é realizado ao longo do mesmo.

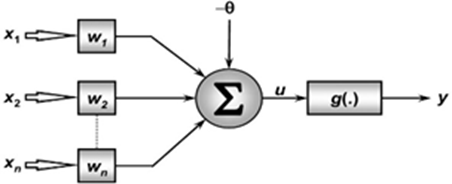
Tendo por base este modelo as RNA foram desenvolvidas com o mesmo principio tendo como componentes básicas unidades de processamento simples a que foi dado o nome de neurónios artificiais ilustrado a seguir na figura 3 :

Figura 3 - Esquema de um neurónio artificial.

As redes neuronais artificiais, consistem em programas únicos de software que imitam a ciência de um neurónio.

A conjugação de vários input (dendrites), num determinado centro de processamento (corpo do neurónio).

Este último tem um determinado threshold, que é valor a partir do qual fica excitado e envia um sinal positivo para o processo seguinte. Este valor pode variar entre os vários centros de processamento. Assim, o output irá depender da multiplicação dos valores e pesos dos múltiplos inputs.

Este conjunto de valores irá dar resultado a um valor final que pode ou não ultrapassar o threshold e desta forma levar a um sinal positivo (1) ou negativo (0), que produz uma contribuição para um estado excitatório ou inibitório, respetivamente .

Uma rede neuronal artificial está, por norma, organizada em camadas, sendo que todos os neurônios de uma determinada camada têm de estar inter-conectados com um neurônio da camada subsequente.

Assim, os neurónios da primeira camada terão o nome de neurónios de input, os das camadas intermédias têm a designação de camadas escondidas e os da última camada serão neurónios de output.

Uma das principais características das RNA a sua capacidade de aprendizagem e de treino , através de algoritmos desenvolvidos para o efeito, sendo os mesmos elaborados por um conjunto de regras bem definidas que influenciam a forma como deve ser alterado o valor de cada peso.

Um dos principias algoritmos de treino foi o desenvolvido por (Rumelhar et al, 1986) baseado em gradientes descendentes a que de seu o nome de Back-propagation . Este algoritmo permitiu a massificação da utilização das redes multi camadas já que permitiu o seu treinamento.

O processo de treino no caso especifico deste algoritmo assenta num processo iterativo que constituído por duas etapas ; uma para a frente (forward) e uma par trás (backward) . Na primeira fase cada objeto de entrada é dado a conhecer à rede. O mesmo é recebido por cada um dos neurónios da primeira camada intermediaria sendo ponderado pelo peso associado à conexão de entrada correspondente . Na camada respetiva cada neurônio pertencente à mesma aplica a função de ativação à soma das suas entradas a produz um valor de saída (output) que é utilizado como valor de entrada (input) da camada de neurónios seguinte. Este processo é continuo ate que os neurónios da camada de saída produzem eles mesmos o seu valor de saída. Este valor é então comparado com o valor de com o valor esperado para saída desse neurônio. A diferença entre os valores achados é o erro cometido pela rede para o objeto introduzido na rede.

A equação seguinte indica como é feito o ajuste de pesos de uma rede MLP pelo algoritmo back-propagation

Exemplo de algoritmo de treino back-propagation

• Entrada : um conjunto de n objetos de treino
• Saída : Rede MPL com valores de pesos ajustados
• inicializar pesos da rede com valores aleatórios
• inicializar erro total=0
• repita
  • para cada objeto xi do conjunto faça
    • para cada camada de rede , a partir da primeira camada intermediaria.
      • Faça para cada neurónio njl da camada:
        • calcular valor da saída produzida pelo neurónio , f
      • fim
    • fim
    • calcular erro parcial=y-f
    • para cada camada de rede a partir da camada de saída faça:
      • para cada neurónio njl da camada faça
        • ajustar pesos do neurónio utilizando Equação
      • fim
    • fim
    • calcular erro total = erro total + erro parcial
  • fim
• até erro total <

Exemplos Rapidminer

• 

  Árvore de decisão e respetivo teste de performance

• 

  Cross-Validation de uma árvore de decisão

• 

  Processo de Cross-Validation

• 

  Resultado de performance de uma árvore de decisão

• 

  Exemplo com todos os métods abordados

Conclusão

The final solution was accomplished by combining many independent models developed by different teams that joined forces. It highlights the power of using ensembles to combine a heterogeneous set of models to achieve maximum accuracy.

Referências

Miguel Duarte, João Sabino, Mário Leal e Ricardo Lourenço 05h19min de 22 de fevereiro de 2016 (CET)